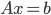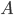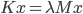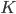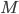My master's thesis deals with dense and sparse solvers for generalized eigenvalue problems (GEPs) with Hermitian positive semidefinite matrices. Key results are
- structure-preserving backward error bounds computable in linear time,
- the runtime of GSVD-based dense GEP solvers is within factor 5 of the fastest GEP solver with Netlib LAPACK in my tests,
- computing the GSVD directly is up to 20 times slower than the computation by means of QR factorizations and the CS decomposition with Netlib LAPACK in my tests,
- given a pair of matrices with 2x2 block structure, I show how to minimize eigenvalue perturbation by off-diagonal blocks with the aid of graph algorithms, and
- I propose a new multilevel eigensolver for sparse GEPs that is able to compute up to 1000 eigenpairs on a cluster node with two dual-core CPUs and 16 GB virtual memory limit for problems with up to 150,000 degrees of freedom in less than eleven hours.
The revised edition of the thesis with fixed typos is here (PDF), the source code is available here, and the abstract is below. In February, I already gave a talk on the preliminary thesis results; more details can be found in the corresponding blog post.
Abstract
This thesis treats the numerical solution of generalized eigenvalue problems (GEPs)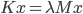 
, where 
, 
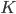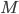are Hermitian positive semidefinite (HPSD). We discuss problem and solution properties, accuracy assessment of solutions, aspect of computations in finite precision, the connection to the finite element method (FEM), dense solvers, and projection methods for these GEPs. All results are directly applicable to real-world problems.
We present properties and origins of GEPs with HPSD matrices and briefly mention the FEM as a source of such problems.
With respect to accuracy assessment of solutions, we address quickly computable and structure-preserving backward error bounds and their corresponding condition numbers for GEPs with HPSD matrices. There is an abundance of literature on backward error measures possessing one of these features; the backward error in this thesis provides both.
In Chapter 3, we elaborate on dense solvers for GEPs with HPSD matrices. The standard solver reduces the GEP to a standard eigenvalue problem; it is fast but requires positive definite mass matrices and is only conditionally backward stable. The QZ algorithm for general GEPs is backward stable but it is also much slower and does not preserve any problem properties. We present two new backward stable and structure preserving solvers, one using deflation of infinite eigenvalues, the other one using the generalized singular value decomposition (GSVD). We analyze backward stability and computational complexity. In comparison to the QZ algorithm, both solvers are competitive with the standard solver in our tests. Finally, we propose a new solver combining the speed of deflation with the ability of GSVD-based solvers to handle singular matrix pencils.
Finally, we consider black-box solvers based on projection methods to compute the eigenpairs with the smallest eigenvalues of large, sparse GEPs with Hermitian positive definite matrices (HPD). After reviewing common methods for spectral approximation, we briefly mention ways to improve numerical stability. We discuss the automated multilevel substructuring method (AMLS) before analyzing the impact of off-diagonal blocks in block matrices on eigenvalues. We use the results of this thesis and insights in recent papers to propose a new divide-and-conquer eigensolver and to suggest a change that makes AMLS more robust. We test the divide-and-conquer eigensolver on sparse structural engineering matrices with 10,000 to 150,000 degrees of freedom.
2010 Mathematics Subject Classification. 65F15, 65F50, 65Y04, 65Y20.
Edit: Revised master's thesis from April 2016 (PDF)
, 
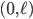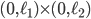, and so on (hyperrectangles) with zero Dirichlet boundary conditions discretized with the finite difference method (FDM) and the finite element method (FEM) on equidistant grids. For the FDM discretization, we use the central differences scheme with the standard five-point stencil in 2D. For the FEM, the ansatz functions are the hat functions. The matrices, standard eigenvalue problems 
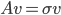, and generalized eigenvalue problems 
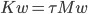arising from the discretization lend themselves for test problems in numerical linear algebra because they are well-conditioned, not diagonal, and the matrix dimension can be increased arbitrarily.
