In this blog post, I present stiffness and mass matrix as well as eigenvalues and eigenvectors of the Laplace operator (Laplacian) on domains 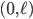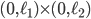$(0, \ell)$, $(0, \ell_1) \times (0, \ell_2)$, and so on (hyperrectangles) with zero Dirichlet boundary conditions discretized with the finite difference method (FDM) and the finite element method (FEM) on equidistant grids. For the FDM discretization, we use the central differences scheme with the standard five-point stencil in 2D. For the FEM, the ansatz functions are the hat functions. The matrices, standard eigenvalue problems 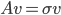$A v = \sigma v$, and generalized eigenvalue problems 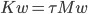$K w = \tau M w$ arising from the discretization lend themselves for test problems in numerical linear algebra because they are well-conditioned, not diagonal, and the matrix dimension can be increased arbitrarily.

Python code generating the matrices and their eigenpairs can be found in my git repository discrete-laplacian.

Continue reading The Discretized Laplace Operator on Hyperrectangles with Zero Dirichlet Boundary Conditions →