In this blog post, I present stiffness and mass matrix as well as eigenvalues and eigenvectors of the Laplace operator (Laplacian) on domains 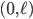 ,
, 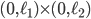 , and so on (hyperrectangles) with zero Dirichlet boundary conditions discretized with the finite difference method (FDM) and the finite element method (FEM) on equidistant grids. For the FDM discretization, we use the central differences scheme with the standard five-point stencil in 2D. For the FEM, the ansatz functions are the hat functions. The matrices, standard eigenvalue problems
, and so on (hyperrectangles) with zero Dirichlet boundary conditions discretized with the finite difference method (FDM) and the finite element method (FEM) on equidistant grids. For the FDM discretization, we use the central differences scheme with the standard five-point stencil in 2D. For the FEM, the ansatz functions are the hat functions. The matrices, standard eigenvalue problems 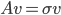 , and generalized eigenvalue problems
, and generalized eigenvalue problems 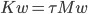 arising from the discretization lend themselves for test problems in numerical linear algebra because they are well-conditioned, not diagonal, and the matrix dimension can be increased arbitrarily.
arising from the discretization lend themselves for test problems in numerical linear algebra because they are well-conditioned, not diagonal, and the matrix dimension can be increased arbitrarily.
Python code generating the matrices and their eigenpairs can be found in my git repository discrete-laplacian.
Introduction
Let 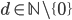 , let
, let 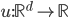 . The differential operator
. The differential operator  is called Laplacian and it is the sum of the second derivatives of a function:
is called Laplacian and it is the sum of the second derivatives of a function:
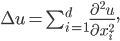
It is a well-researched differential operator in mathematics and for many domains, the exact eigenvalues 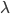 and eigenfunctions
and eigenfunctions 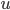 are known such that
are known such that
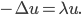
In this blog post, I discuss the solutions of 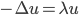 on hyperrectangles
on hyperrectangles 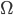 with the Dirichlet boundary condition
with the Dirichlet boundary condition
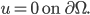
The combination of Laplace operator and the finite difference method (FDM) can be very well used in an introductory course on the numerical treatment of partial differential equations (PDEs) for the illustration of concepts such as discretization of PDEs, discretization error, the growth of the matrix condition number with finer grids, and sparse solvers.
In numerical linear algebra, the Laplace operator is appealing because the FDM discretization of the operator on a one-dimensional domain yields a standard eigenvalue problem 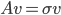 with a sparse, real symmetric positive-definite, tridiagonal Toeplitz matrix
with a sparse, real symmetric positive-definite, tridiagonal Toeplitz matrix 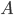 and known eigenpairs. For domains in higher dimensions, the matrices can be constructed with the aid of the Kronecker sum and consequently, the eigenpairs can be calculated in this case, too. With this knowledge, the Laplace operator makes for a good, easy test problem in numerical mathematics because we can distinguish between discretization errors and algebraic solution errors. Naturally, the Laplace operator can also be discretized with the finite element method (FEM) yielding a generalized eigenvalue problem
and known eigenpairs. For domains in higher dimensions, the matrices can be constructed with the aid of the Kronecker sum and consequently, the eigenpairs can be calculated in this case, too. With this knowledge, the Laplace operator makes for a good, easy test problem in numerical mathematics because we can distinguish between discretization errors and algebraic solution errors. Naturally, the Laplace operator can also be discretized with the finite element method (FEM) yielding a generalized eigenvalue problem 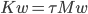 with sparse, real symmetric positive-definite matrices. Here, the eigenpairs are known, too, and furthermore, the eigenvectors are exact in the grid points (so-called superconvergence) providing us with another well-conditioned test problem.
with sparse, real symmetric positive-definite matrices. Here, the eigenpairs are known, too, and furthermore, the eigenvectors are exact in the grid points (so-called superconvergence) providing us with another well-conditioned test problem.
I will present the solutions for the continuous case before I briefly introduce Kronecker products and Kronecker sums since these linear algebra operations are used to construct the matrices corresponding to higher dimensional domains. Finally, I discuss domain discretization and notation before giving closed expressions for the matrices and their eigenpairs created by FDM and FEM. In the end, there is an example demonstrating the use of the quantities 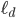 ,
, 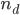 , and
, and  .
.
Continuous Case
In 1D, the exact eigenpairs 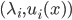 of the Laplace operator on the domain
of the Laplace operator on the domain 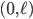 are
are
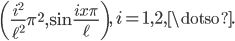
In 2D, the exact eigenpairs 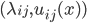 of the Laplace operator on the domain
of the Laplace operator on the domain 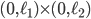 are
are
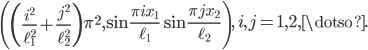
On a 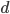 -dimensional hyperrectangle, the eigenpairs are
-dimensional hyperrectangle, the eigenpairs are
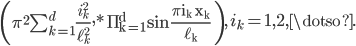
These solutions can be found, e.g., in the book Methods of Mathematical Physics, Vol. I, Chapter VI, §4.1.
Kronecker Products
The matrices of the discretized Laplacian on higher dimensional domains can be constructed with Kronecker products. Given two matrices ![A = [a_{ij}] \in \mathbb{R}^{m,n}](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_192dcf2f874658b8080ae65d8c1a16e2.gif) ,
,  , the Kronecker product
, the Kronecker product 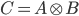 is defined as follows:
is defined as follows:
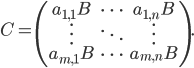
If 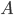 and
and 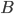 are square, then
are square, then 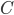 is square as well; let
is square as well; let 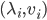 be the eigenpairs of
be the eigenpairs of 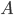 and let
and let 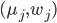 be the eigenpairs of
be the eigenpairs of 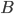 . Then the eigenpairs of
. Then the eigenpairs of 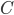 are
are
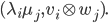
If 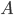 and
and 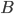 are real symmetric, then
are real symmetric, then 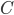 is also real symmetric. For square
is also real symmetric. For square 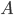 and
and 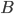 , the Kronecker sum of
, the Kronecker sum of 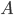 and
and 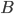 is defined as
is defined as
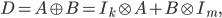
where 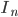 is the
is the 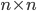 identity matrix. The eigenvalues of
identity matrix. The eigenvalues of 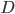 are
are
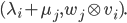
The Kronecker sum occurs during the construction of the 2D FDM matrix. See, e.g., Matrix Analysis for Scientists and Engineers by Alan J. Laub, Chapter 13, for more information on these operations.
Domain Discretization
For the 1D case along the 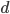 -th axis, we use
-th axis, we use 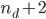 points uniformly distributed over
points uniformly distributed over 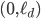 , such that the step size is
, such that the step size is 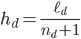 . We use lexicographical ordering of points, e.g., in 2D let
. We use lexicographical ordering of points, e.g., in 2D let 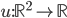 be an eigenfunction of the continuous problem, let
be an eigenfunction of the continuous problem, let 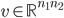 be an eigenvector of the algebraic eigenvalue problem. Then
be an eigenvector of the algebraic eigenvalue problem. Then 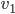 is an approximation to
is an approximation to 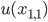 ,
, 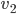 approximates
approximates 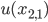 ,
, 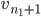 approximates
approximates 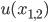 , and so on.
, and so on.
To obtain accurate approximations to the solutions of the continuous eigenvalue problem, the distance between adjacent grid points should always be constant. Thus, if the length of the 1D domain is doubled, the number of grid points should be doubled, too.
Notation
In the following sections, we need to deal with matrices arising from discretizations of the Laplace operator on 1D domains with different step sizes and their eigenpairs as well as discretizations of the Laplace operator on higher dimensional domains and their eigenpairs. 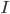 denotes the identity matrix; its dimension can be gathered from the context.
denotes the identity matrix; its dimension can be gathered from the context.
Matrices 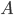 denote the Laplacian discretized with the FDM, matrices
denote the Laplacian discretized with the FDM, matrices  denote the discrete Laplacian on 1D domains along the
denote the discrete Laplacian on 1D domains along the 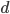 -th axis, and matrices
-th axis, and matrices 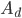 denote the the discrete Laplacian on a
denote the the discrete Laplacian on a 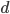 -dimensional domain. The eigenpairs of
-dimensional domain. The eigenpairs of 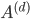 are signified by
are signified by 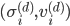 ,
, 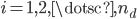 ,
, 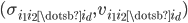 are the eigenpairs of
are the eigenpairs of 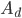 .
.
Similarly, 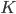 and
and 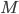 are the stiffness and mass matrix, respectively, of the Laplace operator discretized with the finite element method.
are the stiffness and mass matrix, respectively, of the Laplace operator discretized with the finite element method. 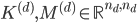 denote the discrete Laplacian on a one-dimensional domain along the
denote the discrete Laplacian on a one-dimensional domain along the 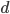 -th axis, and
-th axis, and 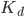 ,
, 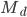 are the stiffness and mass matrix for the discrete Laplacian on a
are the stiffness and mass matrix for the discrete Laplacian on a 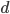 -dimensional hyperrectangle. We speak of the solutions of
-dimensional hyperrectangle. We speak of the solutions of 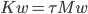 or of eigenpairs of the matrix pencil
or of eigenpairs of the matrix pencil 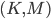 . The eigenpairs of
. The eigenpairs of 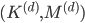 are denoted by
are denoted by 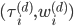 , whereas
, whereas 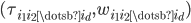 signify eigenpairs of
signify eigenpairs of 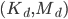 .
.
Finite Difference Method
In this section, we will construct the matrices of the discretized Laplace operator on a 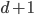 -dimensional domain with the aid of the matrices for the
-dimensional domain with the aid of the matrices for the 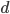 -dimensional and the one-dimensional case.
-dimensional and the one-dimensional case.
Let 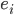 be the
be the 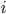 -th unit vector. Let us consider the discretization along the
-th unit vector. Let us consider the discretization along the 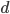 -th axis first. Let
-th axis first. Let
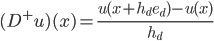
be the forward difference quotient, let
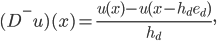
be the backward difference quotient. Then
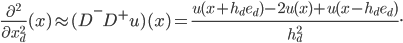
Consequently, the discrete Laplacian has the stencil
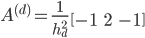
meaning 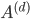 is a real symmetric tridiagonal
is a real symmetric tridiagonal 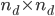 matrix with the value 2 on the diagonal and -1 on the first sub- and superdiagonal. The eigenvalues of
matrix with the value 2 on the diagonal and -1 on the first sub- and superdiagonal. The eigenvalues of 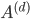 are
are
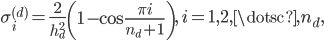
the entries of the eigenvector 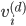 are
are
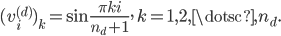
In 2D with lexicographic ordering of the variables, we have
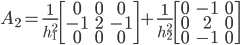
and this matrix can be constructed as follows:
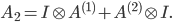
The eigenpairs can be derived directly from the properties of the Kronecker sum: the eigenvalues are
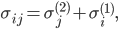
and the eigenvectors are
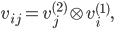
where 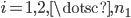 ,
, 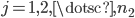 .
.
In higher dimensions, it holds that
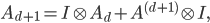
where
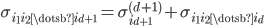
are the eigenvalues and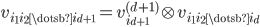
are the eigenvectors, 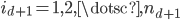 .
.
Finite Element Method
Similarly to the finite differences method, we can construct the matrices of the discretized equation 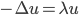 recursively. We use hat functions as ansatz functions throughout this section.
recursively. We use hat functions as ansatz functions throughout this section.
The 1D stencil is
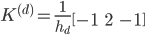
for the stiffness matrix and
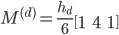
for the mass matrix. The generalized eigenvalues are
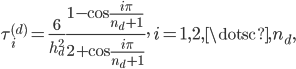
and the 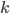 -th entry of the eigenvector
-th entry of the eigenvector 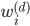 corresponding to
corresponding to 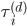 is
is
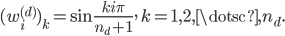
Observe that 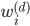 is not only an eigenvector of the matrix pencil
is not only an eigenvector of the matrix pencil 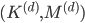 but also of the matrices
but also of the matrices 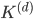 and
and 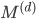 themselves. Thus, the eigenvalues of
themselves. Thus, the eigenvalues of 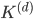 are
are

whereas the eigenvalues of 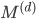 are
are
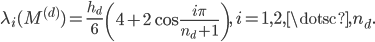
In 2D, the mass matrix stencil is
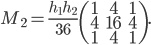
Judging by the coefficient 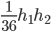 and the diagonal blocks, it must hold that
and the diagonal blocks, it must hold that
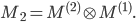
The stiffness matrix stencil is
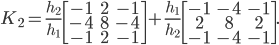
Seeing the factors 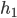 and
and 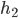 , the stiffness matrix cannot be the Kronecker product or the Kronecker sum of 1D stiffness matrices. However, observe that the 1D mass matrices
, the stiffness matrix cannot be the Kronecker product or the Kronecker sum of 1D stiffness matrices. However, observe that the 1D mass matrices 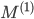 and
and 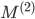 have coefficients
have coefficients 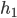 and
and 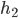 , respectively, and indeed, the 2D stiffness matrix can be constructed with the aid of the 1D mass matrices:
, respectively, and indeed, the 2D stiffness matrix can be constructed with the aid of the 1D mass matrices:
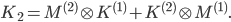
Based on the properties of the Kronecker product and using the fact that mass and stiffness matrix have the same set of eigenvalues, 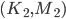 has the eigenvalues
has the eigenvalues
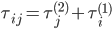
and eigenvectors
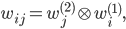
where 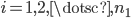 ,
, 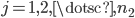 .
.
For the Laplacian on hyperrectangles in 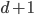 -dimensional space, the stiffness matrix can be constructed by
-dimensional space, the stiffness matrix can be constructed by
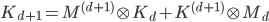
the mass matrix can be constructed using
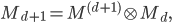
such that 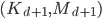 has eigenvalues
has eigenvalues
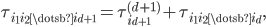
and eigenvectors
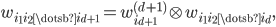
where 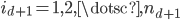 .
.
Example
Now I will present the matrices of the discrete Laplacian on the domain 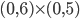 . The figure below shows the domain and the grid used for discretization: there are five interior grid points along the first axis, three interior points along the second axis, and the interior grid points are highlighted as black circles. Thus,
. The figure below shows the domain and the grid used for discretization: there are five interior grid points along the first axis, three interior points along the second axis, and the interior grid points are highlighted as black circles. Thus, 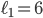 ,
, 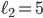 ,
, 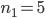 ,
, 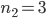 , the step size
, the step size 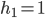 , and
, and 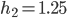 . In 2D, an eigenvector
. In 2D, an eigenvector 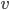 of the algebraic eigenvalue problem will possess entries
of the algebraic eigenvalue problem will possess entries 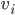 ,
, 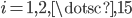 , such that
, such that 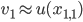 ,
, 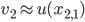 ,
, 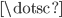 ,
, 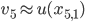 ,
, 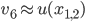 ,
,  ,
, 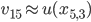 because of the lexicographic ordering.
because of the lexicographic ordering.

In the first dimension, the Laplacian discretized with the FDM has the following matrix:
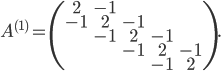 Along the second axis, we have
Along the second axis, we have
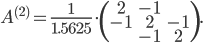
With the FEM, the stiffness matrix is
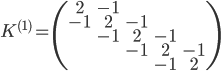
and the mass matrix is
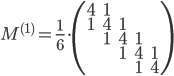
along the first axis. The matrices corresponding to the second dimension are
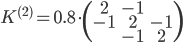
and
