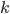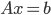Tag Archives: benchmark

Faster RANLUX Pseudo-Random Number Generators

RANLUX denotes a class of high-quality pseudo-random number generators (PRNGs) with long periods, solid theoretical foundations, and uses in computational physics. These generators are built on top of add-with-carry and subtract-with-borrow PRNGs which allow customization through three user-provided parameters yet there are only two variants in use today working internally with 24-bit and 48-bit arithmetic; this comes at a cost because modern computers do not possess instructions for 24-bit or 48-bit arithmetic. In this blog post I will present the theory behind RANLUX PRNGs, a list of possible parameters for 16-, 32-, and 64-bit RANLUX generators, criteria for selecting generators as well as benchmarks comparing the most competitive RANLUX variants with the RANLUX generators in the C++11 standard library, the Mersenne Twister, and xoshiro128+.

Some of the new RANLUX flavors are easily implemented in C++11 (sometimes in only two lines of code), they are  faster than the existing RANLUX flavors, they retain all desirable properties of a RANLUX generator, and they pass all DieHarder and TestU01 BigCrush PRNG tests.

The programs used to compute the RANLUX parameters are called ranlux-tools. They are free software under the terms of the Mozilla Public License 2.0 and can be found online:

https://christoph-conrads.name/software/ranlux-tools

Continue reading Faster RANLUX Pseudo-Random Number Generators →

SuperLU vs Direct Substructuring

The eigenproblem solver in my master's thesis used SuperLU, a direct solver for the solution of systems of linear equations (SLE) Ax = b. For the largest test problems, the eigensolver ran out of memory when decomposing the matrix A which is why I replaced SuperLU with direct substructuring in an attempt to reduce memory consumption. For this blog post, I measured set-up time, solve time, and memory consumption of SuperLU and direct substructuring with real symmetric positive definite real-world matrices for SLEs with a variable number of right-hand sides, I will highlight that SuperLU was deployed with a suboptimal parameter choice, and why the memory consumption of the decomposition of A is the wrong objective function when you want to avoid running out of memory.

Continue reading SuperLU vs Direct Substructuring →

Performance and Accuracy of xPTEQR

xPTEQR is a LAPACK function for the computation of the  eigendecomposition of a symmetric positive definite tridiagonal matrix. I compare the performance and accuracy of xPTEQR to the other symmetric eigensolvers in LAPACK 3.5.0.

In layman’s terms, there are several algorithms available on a computer that calculate the eigenvectors and eigenvalues of matrices with special properties (symmetric, positive definite, tridiagonal). xPTEQR is the name of the computer implementation of one of those algorithms and I am not aware of any measurements with it. In this blog post I compare xPTEQR in terms of speed and accuracy to other good algorithms. In the figures below, xPTEQR can be found under the label "SVD" (xPTEQR is the name of the implementation, SVD is the algorithm). Moreover, in every figure it holds that lower is better.

Continue reading Performance and Accuracy of xPTEQR →