Higham's Accuracy and Stability of Numerical Algorithms is regularly needed for my work. The second edition of the book was released in 2002 so some of the bounds do not reflect the state of the art in 2015. I collected some papers with improved bounds which are relevant for me.
See the table below for the improvements. Kiełbasiński's 1987 paper is cited in Higham's book but his bounds were not used which is why they can be found in the table below. Rump's 2012 paper Error estimation of floating-point summation and dot product (DOI:10.1007/s10543-011-0342-4) presents error bounds for the inner product and summation only for radix 2 and recursive summation but he also describes the computation of upper bounds on the error in finite precision arithmetic. Note that Lemma 8.4 is used throughout the book and with it one can, for example, find a simple bound for the spectral norm of the backward error of the Cholesky decomposition in Theorem 10.3:
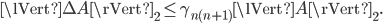
Do not confuse this bound with inequality (10.7) in Higham's book which refers to Theorem 10.4.
| Location | Topic | Improvement | Source |
|---|---|---|---|
| §2 | Floating point arithmetic | Refinement of the standard floating point model resulting in tighter error bounds | Link |
| §3.1 | Inner products | Simple, sharp error bounds for any radix, any evaluation order without restrictions on the dimension | Link |
| §4.1 | Summation | Simple, sharp error bounds for any radix, any evaluation order without restrictions on the dimension | Link |
| Lemma 8.4 | Triangular systems | Simpler, sharper error bounds for any radix, any evaluation order without restrictions on the dimension | Link |
| §10.1.1 | Cholesky factorization | "Almost sharp" bound on the Frobenius norm of the backward error, a condition for guaranteed completion | Link |
| §10.5.1 | Cholesky factorization | LAPACK implementation of Cholesky factorization for positive semidefinite matrices xPSTRF | Link |
| §19.8 | Gram-Schmidt algorithm | Bounds on the loss of orthogonality of the Q factor for CGS2 (two iterations of classical Gram-Schmidt) | Link |