xPTEQR is a LAPACK function for the computation of the  eigendecomposition of a symmetric positive definite tridiagonal matrix. I compare the performance and accuracy of xPTEQR to the other symmetric eigensolvers in LAPACK 3.5.0.

In layman’s terms, there are several algorithms available on a computer that calculate the eigenvectors and eigenvalues of matrices with special properties (symmetric, positive definite, tridiagonal). xPTEQR is the name of the computer implementation of one of those algorithms and I am not aware of any measurements with it. In this blog post I compare xPTEQR in terms of speed and accuracy to other good algorithms. In the figures below, xPTEQR can be found under the label "SVD" (xPTEQR is the name of the implementation, SVD is the algorithm). Moreover, in every figure it holds that lower is better.

Introduction

xPTEQR is a special eigensolver in LAPACK because it uses several other algorithms to compute the eigendecomposition instead of implementing a certain algorithm like xSTEQR (Francis QR) or xSTEDC (Divide & Conquer). xPTEQR first calculates a Cholesky decomposition of the matrix at hand before computing the singular value decomposition of the lower triangular factor. Since I was unable to find xPTEQR benchmarks comparing it to the other symmetric eigensolvers in LAPACK I decided to do the comparison myself. There is an article from 2007 called "Performance and Accuracy of LAPACK's Symmetric Tridiagonal Eigensolvers" benchmarking LAPACK’s eigensolvers for general symmetric matrices but naturally xPTEQR is not considered.

In this blog post I will compare the symmetric eigensolvers in the LAPACK reference implementation (Netlib LAPACK) with xPTEQR in terms of relative speed and accuracy. Moreover, I will explicitly mention how xPTEQR compares to xSTEQR because the SVD algorithm used by xPTEQR is implicitly using the Francis QR algorithm (hence the same suffix).

Test Setup

For the measurements I will use stetester, a testing infrastructure for LAPACK’s symmetric eigensolvers (I explained how to compile stetester in a previous blog post). This program takes care of most tasks required for benchmarking:

• it creates the synthetic test matrices,
• it compensates for very short run-times, and
• it calculates the accuracy of the computed eigenvectors and eigenvalues.

By default stetester does not test xPTEQR hence I patched the software. Following the article "Performance and Accuracy of LAPACK's Symmetric Tridiagonal Eigensolvers", I performed the tests with synthetic and real-world matrices. The synthetic matrices have the the 2-condition number 1/u, where u is the unit roundoff, and all deterministic eigenvalue distributions implemented in stetester were tested once using the default seed for the random number generator. For the real-world test problems all BCS structural engineering stiffness matrices from the Harwell-Boeing collection with less than 5000 degrees of freedom were tested. These matrices were tridiagonalized with Matlab. The algorithms had to compute eigenvalues and eigenvectors, no subset computations were performed, and all tests were done in double precision; therefore 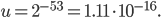$u = 2^{-53} = 1.11 \cdot 10^{-16}.$

To assess the accuracy, stetester computes the residual for each eigenpair and the smallest angle between each eigenvector (all eigenvectors must be pairwise orthogonal in theory). For the measurements of the accuracy the maximum norm was employed. This is neither mentioned in the stetester documentation nor in the article cited above and I had to take a look at the stetester source code to find out (see the file dstechkrslt.F).

The test machine was a computer with 4GB RAM and an Intel Core 2 Duo E6750 CPU. I used Netlib LAPACK 3.5.0 and its corresponding BLAS release (BLAS is part of every LAPACK release). There was a soft 3500MB virtual memory limit.

Note that the cited articles both mention the "machine epsilon ε". There is no general consensus whether machine epsilon and unit roundoff are the same or not. For one side, ε = 2u so that the machine epsilon is the smallest floating point number such that 1 + ε > 1, whereas for the other side, ε = u. The authors of the cited articles belong to the latter group. The Wikipedia article
on the machine epsilon also discussess this issue.

Results

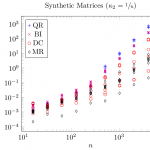
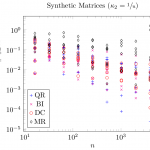
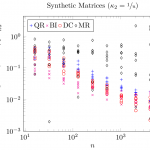
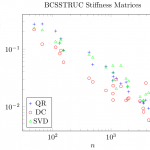
First of all, I plotted time, residual, and loss of orthogonality of the symmetric eigensolvers over the matrix size similarly to the aforementioned article to check if my measurements are consistent with the existing measurements.

The qualitative match between the accuracy plots is good: on average,

• the MRRR algorithm (MR) has the worst accuracy,
• Divide & Conquer (DC) and bisection combined with inverse iteration (BI) are the most accurate methods,
• QR shows good accuracy but not as good as BI and DC.

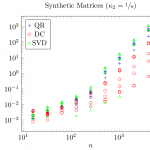
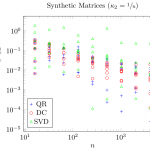
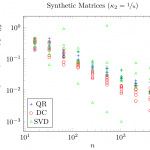
To avoid cluttering the plots with too many colors and symbols, only DC, QR, and xPTEQR (abbreviated as "SVD") will be shown from now on.

xPTEQR has an obvious issue: it must successfully compute a Cholesky decomposition of the matrix at hand, otherwise it cannot calculate the eigendecomposition. For the synthetic test matrices with condition number 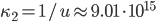$\kappa_2 = 1/u \approx 9.01 \cdot 10^{15}$ success of the Cholesky decomposition is not guaranteed and DPTEQR (the double precision implementation of xPTEQR) did not complete in 13 out of 63 test cases. This is a real drawback.

 

As expected, the SVD run-time is comparable to QR though DC clearly wins this comparison. With respect to the accuracy, SVD can be best described as unsteady: depending on the test case, the accuracy of SVD may be magnitudes better, magnitudes worse, or similar to that of DC and QR. In comparison, QR occasionally computes eigenpairs with residuals that are magnitudes smaller than the average residual for fixed n but it has no outliers in the other direction. Overall, DC is clearly the most accurate and most stable method of the three for matrices with at least 100 degrees of freedom.

 

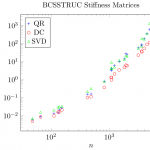
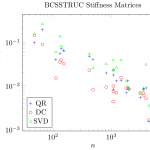
For the real-world matrices, the Cholesky decomposition always completed. This is the upside when using SVD. The downside is that QR is comparable in speed to SVD while DC is consistenly faster than SVD. At the same time, QR and DC are with one exception at least as accurate as SVD, that is, both residual and loss of orthogonality are smaller.

Conclusion

xPTEQR cannot be recommended as eigensolver. The Cholesky decomposition may fail and with Divide & Conquer there is at least one eigensolver for general symmetric matrices that is consistently faster. xPTEQR requires a small workspace of 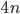$4n$ which is underbid by xSTEQR, the LAPACK implementation of the QR algorithm, with 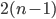$2(n - 1)$ therefore if low memory consumption is at a premium xPTEQR is not the method of choice either.

LAPACK features an SVD solver based on Divide & Conquer called xBDSDC. Motivated by the plots above I wonder if xPTEQR would perform better in terms of speed and accuracy if it were to use xBDSDC (the memory consumption is bound to skyrocket).

Tools

The test results were produced with BLAS, LAPACK 3.5.0, and stetester. The stetester output was postprocessed with GNU AWK and the results were plotted with pgfplots. The PDF plots were converted to PNG with pdftocairo which is part of Poppler.

Links

• Download stetester (880.zip) @ acm.org
• Download stetester (880.zip) @ netlib.org
• Harwell-Boeing Sparse Matrix Collection @ UF Sparse Matrix Collection

Edit April 15, 2016

The measurement data and the LaTeX files of the plots are available on gitlab.com.

Edit February 27, 2015

After I finished this post, I started to wonder why xPTEQR was included in LAPACK in the first place. The answer can be found in LAPACK Working Note (LAWN) 7. The first sentence of the abstract reads:

When computing eigenvalues of symmetric matrices and singular values of general matrices in finite precision arithmetic we in general only expect to compute them with an error bound proportional to the product of machine precision and the norm of the matrix.

It turns out that the QR algorithm in 1990 only computed eigenvalues with a small absolute error instead of a small relative error. xPTEQR can be found in LAWN 7 as algorithm 2 (page 24) and it enabled the existing QR algorithm to deliver high relative accuracy. I tried to put the information in LAWN 7 into perspective with the following timeline:

• The Francis' QR algorithm appears in 1961 (Paper Part I, Part II freely accessible by courtesy of The Computer Journal),
•  Cuppen's paper on Divide & Conquer was published in 1981,
• LAWN 7 is published in 1990,
• LAPACK 1.0 was released in February 1992 and contained xPTEQR, bisection,
• the first LAPACK release with Divide & Conquer was LAPACK 2.0, September 1994,
• Dhillon finished his PhD thesis about MR in 1997,
• the first LAPACK to contain the MR algorithm was LAPACK 3.0, June 1999.