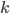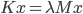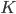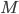RANLUX denotes a class of high-quality pseudo-random number generators (PRNGs) with long periods, solid theoretical foundations, and uses in computational physics. These generators are built on top of add-with-carry and subtract-with-borrow PRNGs which allow customization through three user-provided parameters yet there are only two variants in use today working internally with 24-bit and 48-bit arithmetic; this comes at a cost because modern computers do not possess instructions for 24-bit or 48-bit arithmetic. In this blog post I will present the theory behind RANLUX PRNGs, a list of possible parameters for 16-, 32-, and 64-bit RANLUX generators, criteria for selecting generators as well as benchmarks comparing the most competitive RANLUX variants with the RANLUX generators in the C++11 standard library, the Mersenne Twister, and xoshiro128+.
Some of the new RANLUX flavors are easily implemented in C++11 (sometimes in only two lines of code), they are faster than the existing RANLUX flavors, they retain all desirable properties of a RANLUX generator, and they pass all DieHarder and TestU01 BigCrush PRNG tests.
The programs used to compute the RANLUX parameters are called ranlux-tools. They are free software under the terms of the Mozilla Public License 2.0 and can be found online:
https://christoph-conrads.name/software/ranlux-tools
Continue reading Faster RANLUX Pseudo-Random Number Generators