Given a linear algebra problem and an approximate solution, can we say something about the quality of the given approximate solution without knowing an exact solution?
In this post, let  denote the problem data, let
denote the problem data, let 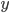 denote an exact solution, let
denote an exact solution, let 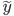 be an approximate solution, and let
be an approximate solution, and let 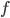 be a mapping such that
be a mapping such that 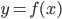 . Moreover, let
. Moreover, let 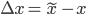 , where
, where 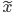 is given in the next paragraph.
is given in the next paragraph. 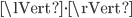 denotes a norm.
denotes a norm.
Bounding the Error
Can we say something about the forward error  without calculating
without calculating  ? The answer is yes, we can say something about the quality of the approximate solution by computing the backward error
? The answer is yes, we can say something about the quality of the approximate solution by computing the backward error 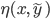 . It gives us the smallest distance between
. It gives us the smallest distance between  and some
and some 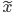 such that
such that 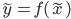 , i.e., the backward error is
, i.e., the backward error is
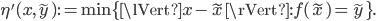
In conjunction with a Taylor series expansion of 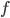 at
at  we can bound the forward error from above. Cutting off the series expansion after the first-order term gives
we can bound the forward error from above. Cutting off the series expansion after the first-order term gives
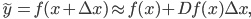
where 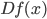 signifies the Jacobian of
signifies the Jacobian of 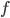 at
at  . Substituting
. Substituting 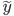 into the definition of the forward error yields
into the definition of the forward error yields
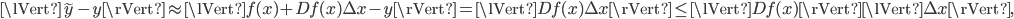
where we used 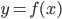 . Defining the condition number
. Defining the condition number
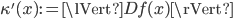
gives
forward error  condition number
condition number 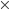 backward error.
backward error.
Depending on its norm, the condition number can have the effect of a magnifier for errors. Note the condition number is problem dependent, i.e., on 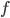 and
and  , but independent of the approximate solution
, but independent of the approximate solution 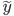 at hand. Consequently, for problems with large condition numbers we cannot expect (in general) a small forward error even if the backward error is tiny. Such problems are called ill-conditioned. Note that for consistency, condition number and backward error must use the same norm.
at hand. Consequently, for problems with large condition numbers we cannot expect (in general) a small forward error even if the backward error is tiny. Such problems are called ill-conditioned. Note that for consistency, condition number and backward error must use the same norm.
Bounding the Relative Error
Above, we defined absolute measures, i.e., the absolute forward error, the absolute condition number, and the absolute backward error. These measures are not scale invariant and this makes it hard for us to determine when an error can be considered small. We can solve this problem by using relative measures:
- the relative forward error
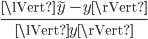 ,
, - the relative backward error
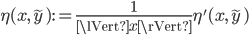 , and
, and - the relative condition number
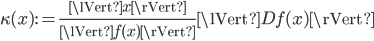 .
.
For the relative backward error, it holds that
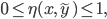
where a value close to zero implies a good approximate solution and a value close to one means that 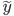 is the solution for a completely different problem. Furthermore, in finite precision arithmetic, i.e, on a computer, we can specify a value
is the solution for a completely different problem. Furthermore, in finite precision arithmetic, i.e, on a computer, we can specify a value 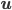 such that every approximate solution with
such that every approximate solution with 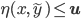 can be considered accurate with respect to finite precision arithmetic. Let
can be considered accurate with respect to finite precision arithmetic. Let 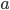 be the smallest, positive number without underflow, let
be the smallest, positive number without underflow, let 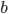 be the largest finite number in finite precision arithmetic, f.e., with IEEE double precision floating point arithmetic,
be the largest finite number in finite precision arithmetic, f.e., with IEEE double precision floating point arithmetic,
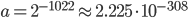
and
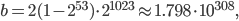
let ![r \in [a, b]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_fd8964452a7df1a415b3bce3360c9776.gif) . Then for the floating point number
. Then for the floating point number 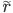 closest to
closest to 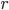 , it holds that
, it holds that
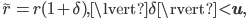
where 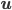 is called unit round-off. This is a relative backward error bound which is more obvious if we rewrite the equation as
is called unit round-off. This is a relative backward error bound which is more obvious if we rewrite the equation as
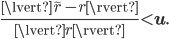
(It is simultaneously a forward error because the condition number is one.) If we cannot expect to represent a single number with a backward error less than 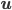 , then we cannot expect to solve any problem with a backward error smaller than
, then we cannot expect to solve any problem with a backward error smaller than 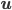 either. Consequently, if the relative backward error is less than
either. Consequently, if the relative backward error is less than 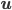 , we found a solution that can be considered as close as possible to an exact solution in finite precision arithmetic. Note the unit round-off
, we found a solution that can be considered as close as possible to an exact solution in finite precision arithmetic. Note the unit round-off 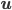 is related to the machine epsilon
is related to the machine epsilon 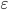 by
by 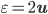 . Also, with IEEE double precision floats,
. Also, with IEEE double precision floats, 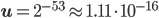 .
.
In general, it is undesirable to directly bound the forward error because bounding the forward error gives weaker bounds on the backward error than the other way around. What is more, for ill-conditioned problems the backward error remains a reliable termination criterion termination while the forward error does not. Thus, our measure for solution quality will be the backward error.
The Backward Error in Practice
Using relative backward errors, we can assess the accuracy of an approximate solution without the need for exact solutions. To put the icing on the cake, for many linear algebra problems there are closed-form expressions for the relative backward error using common and intuitive norms. That is, we can evaluate the quality of a solution by calculating matrix-vector products and vector norms irrespective of the level of difficuly of the problem. For example, for a system of linear equations 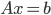 , we have
, we have
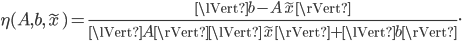
Example: A System of Linear Equations
Consider the SLE 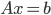 , where
, where
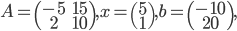
let 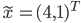 be an approximate solution. Let
be an approximate solution. Let 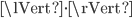 be the maximum norm. Then the backward error is
be the maximum norm. Then the backward error is
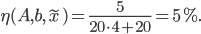
The Backward Error in Practice (cont'd)
For a more complicated generalized eigenvalue problem 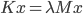 ,
, 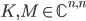 , the relative backward error of an eigenpair
, the relative backward error of an eigenpair 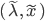 can be calculated with
can be calculated with

Moreover, we can often take problem structure into account which gives us structured backward errors and condition numbers.
Example: Problem Structure and Backward Error
Consider the standard eigenvalue problem 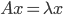 , where
, where
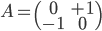
is real skew-symmetric and has the eigenvalues 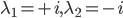 . In this example, we measure the distance between two matrices using the Frobenius norm
. In this example, we measure the distance between two matrices using the Frobenius norm 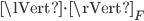 . Consider the approximate eigenvalue
. Consider the approximate eigenvalue 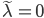 , then
, then
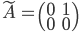
is a matrix closest to 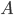 possessing the eigenvalue
possessing the eigenvalue 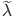 . Consequently,
. Consequently,
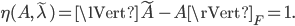
The result is unsatisfying insofar as 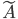 is not skew-symmetric so let us restrict the set of perturbations to the set of real skew-symmetric matrices and let
is not skew-symmetric so let us restrict the set of perturbations to the set of real skew-symmetric matrices and let 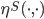 denote the corresponding structured backward error. Then
denote the corresponding structured backward error. Then 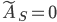 is the matrix closest to
is the matrix closest to 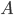 possessing the eigenvalue
possessing the eigenvalue 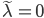 and the structured backward error is
and the structured backward error is 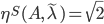 .
.
The Condition Number in Practice
For the relative condition number, we have to make a slight concession: we cannot evaluate it exactly because the exact solution occurs in the denominator. For example, the condition number for linear systems 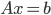 is
is
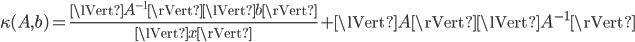
with the solution  appearing in the first term. In practice, this fact is neglected and the approximate solution
appearing in the first term. In practice, this fact is neglected and the approximate solution 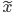 is used. Moreover, we might need to compute matrix norms. This is a simple task for the row sum and the column sum norm but expensive or downright impossible for the spectral norm. In the worst case, we need the norm of a matrix inverse. Luckily, we can estimate this norm for the row sum and the column sum norm.
is used. Moreover, we might need to compute matrix norms. This is a simple task for the row sum and the column sum norm but expensive or downright impossible for the spectral norm. In the worst case, we need the norm of a matrix inverse. Luckily, we can estimate this norm for the row sum and the column sum norm.
Conclusion
In linear algebra we can evaluate the quality of an approximate solution by computing its backward error and the condition number of the problem. In finite precision arithmetic, the backward error is also the method of choice for robust termination criteria.
A comprehensive book about backward errors and condition numbers for many problems in linear algebra is Nicholas J. Higham's Accuracy and Stability of Numerical Algorithms. Unfortunately, it does not discuss eigenvalue problems. Standard eigenvalue problems are discussed in Stewart and Sun's Matrix Perturbation Theory, Higham and Higham's paper Structured Backward Error and Condition of Generalized Eigenvalue Problems deals with generalized eigenvalue problems. Adhikari, Alam, and Kressner present closed-form expressions for the backward error and the condition number for structured polynomial eigenvalue problems in their papers On backward errors of structured polynomial eigenproblems solved by structure preserving linearizations (preprint) and Structured eigenvalue condition numbers and linearizations for matrix polynomials (preprint, verbatim capitalization).
Throughout this post, we used normwise error bounds but for certain problems, we can bound the error for every component of the data. Accordingly, this concept is called the componentwise error in contrast to the normwise error. In the literature, the letters 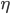 and
and 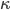 are used to signify both relative and absolute measures because the definition of the backward error is slightly more flexible than in this post; see, f.e., the theorem of Rigal and Gaches in Higham's book "Accuracy and Stability of Numerical Algorithms".
are used to signify both relative and absolute measures because the definition of the backward error is slightly more flexible than in this post; see, f.e., the theorem of Rigal and Gaches in Higham's book "Accuracy and Stability of Numerical Algorithms".