A cover tree is a tree data structure used for the partitiong of metric spaces to speed up operations like nearest neighbor, 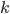 -nearest neighbor, or range searches. In this blog post, I introduce cover trees, their uses, their properties, and I measure the effect of the dimension of the metric space on the run-time in an experiment with synthetic data.
-nearest neighbor, or range searches. In this blog post, I introduce cover trees, their uses, their properties, and I measure the effect of the dimension of the metric space on the run-time in an experiment with synthetic data.
Introduction
Let 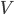 be a set. A function
be a set. A function 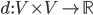 is called a metric for
is called a metric for 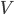 if
if
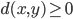 ,
,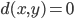 iff
iff 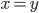 ,
,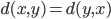 , and
, and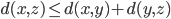 ,
,
where 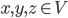 . The last inequality is known as the triangle inequality. The pair
. The last inequality is known as the triangle inequality. The pair 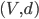 is then called a metric space. Let
is then called a metric space. Let 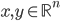 and let
and let 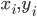 denote the
denote the 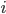 th component of
th component of 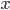 and
and 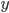 , respectively,
, respectively, 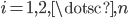 . Often used metrics are the Euclidean metric
. Often used metrics are the Euclidean metric
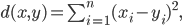
the Manhattan metric
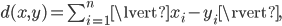
and the Chebychev metric
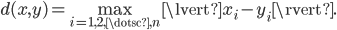
Consider a set of points 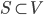 . Given another point
. Given another point 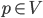 (note that we allow
(note that we allow 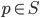 ), we might be interested in the point
), we might be interested in the point 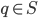 closest to
closest to  ,
, 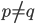 , i.e.,
, i.e.,
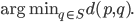
This problem is known as the nearest-neighbor problem. 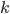 -nearest neighbors is a related problem where we look for the
-nearest neighbors is a related problem where we look for the 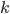 points
points 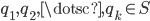 closest to
closest to  ,
, 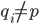 :
:
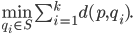
In the all nearest-neighbors problem, we are given sets 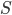 and
and 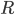 and the goal is to determine the nearest neighbor
and the goal is to determine the nearest neighbor 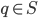 for each point
for each point 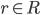 . If
. If 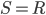 , then we have a monochromatic all nearest-neighbors problem, otherwise the problem is called bichromatic. Finally, there is also the range problem where we are given scalars
, then we have a monochromatic all nearest-neighbors problem, otherwise the problem is called bichromatic. Finally, there is also the range problem where we are given scalars 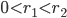 and where we seek the points
and where we seek the points 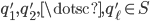 such that
such that 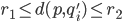 holds for all points
holds for all points 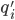 .
.
The nearest-neighbor problem and its variants occur, e.g., during the computation of minimum spanning trees with vertices in a vector space or in 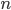 -body simulations, and they are elementary operations in machine learning (nearest centroid classification,
-body simulations, and they are elementary operations in machine learning (nearest centroid classification, 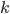 -means clustering, kernel density estimation, ...) as well as spatial databases. Obviously, computing the nearest neighbor using a sequential search requires linear time. Hence, many space-partitioning data structures were devised that were able to reduce the average complexity
-means clustering, kernel density estimation, ...) as well as spatial databases. Obviously, computing the nearest neighbor using a sequential search requires linear time. Hence, many space-partitioning data structures were devised that were able to reduce the average complexity 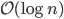 though the worst-case bound is often
though the worst-case bound is often 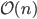 , e.g., for k-d trees or octrees.
, e.g., for k-d trees or octrees.
Cover Trees
Cover trees are fast in practice and have great theoretical significance because nearest-neighbor queries have guaranteed logarithmic complexity and they allow the solution of the monochromatic all-nearest-neighbors problem in linear time instead of 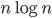 (see the paper Linear-time Algorithms for Pairwise Statistical Problems). Furthermore, cover trees require only a metric for proper operation and they are oblivious to the representation of the points. This allows one, e.g., to freely mix cartesian and polar coordinates, or to use implicitly defined points.
(see the paper Linear-time Algorithms for Pairwise Statistical Problems). Furthermore, cover trees require only a metric for proper operation and they are oblivious to the representation of the points. This allows one, e.g., to freely mix cartesian and polar coordinates, or to use implicitly defined points.
A cover tree 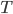 on a data set
on a data set 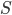 with metric
with metric 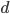 is a tree data structure with levels. Every node in the tree references a point
is a tree data structure with levels. Every node in the tree references a point 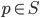 and in the following, we will identify both the node and the point with the same variable
and in the following, we will identify both the node and the point with the same variable  . A cover tree tree
. A cover tree tree 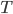 is either
is either
- empty, or
- at level
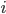 the tree has a single root node
the tree has a single root node  .
.
If  has children, then
has children, then
- the children are non-empty cover trees with root nodes at level
 ,
, - (nesting) there is a child tree with
 as root node,
as root node, - (cover) for the root node
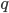 in every child tree of
in every child tree of  , it holds that
, it holds that 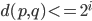 , i.e.,
, i.e.,  covers
covers 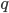 ,
, - (separation) for each pair of root nodes
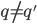 in child trees of
in child trees of  , it holds that
, it holds that 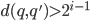 .
.
Note that the cover tree definition does not prescribe that every descendant 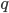 of
of  must have distance
must have distance 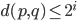 . Let
. Let 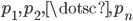 be the parent nodes of
be the parent nodes of 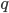 . Then the triangle inequality yields
. Then the triangle inequality yields
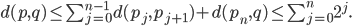
With an infinite amount of levels, we get the inequality
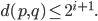
What is more, given a prescribed parent node  , notice that the separation condition implies that child nodes
, notice that the separation condition implies that child nodes 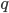 must inserted in the lowest possible level for otherwise we violate the separation inequality
must inserted in the lowest possible level for otherwise we violate the separation inequality 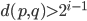 .
.
The definition of the cover trees uses the basis 2 for the definition of the cover radius and the minimum separation but this number can be chosen arbitrarily. In fact, the implementation by Beygelzimer/Kakade/Langford uses the basis 1.3 and MLPACK defaults to 2 but allows user-provided values chosen at run-time. In this blog post and in my implementation I use the basis 2 because it avoids round-off errors during the calculation of the exponent.
Cover trees have nice theoretical properties as you can see below, where 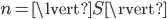 ,
,  denotes the expansion constant explained in the next section:
denotes the expansion constant explained in the next section:
- construction:
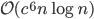 ,
, - insertion:
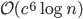 ,
, - removal:
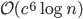 ,
, - query:
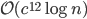 ,
, - batch query:
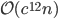 .
.
The cover tree requires 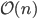 space.
space.
The Expansion Constant 
Let 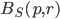 denote the set of points
denote the set of points 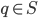 that are less than
that are less than 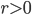 away from
away from  :
:
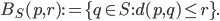
The expansion constant  of a set
of a set 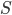 is the smallest scalar
is the smallest scalar 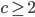 such that
such that
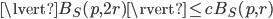
for all  ,
, 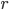 . We will demonstrate that the expansion constant can be large and sensitive to changes in
. We will demonstrate that the expansion constant can be large and sensitive to changes in 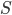 .
.
Let 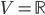 and let
and let
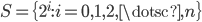
for some integer 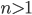 . In this case,
. In this case,  because
because 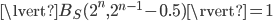 and
and 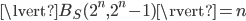 and this is obviously the worst case. Moreover,
and this is obviously the worst case. Moreover,  can be sensitive to changes of
can be sensitive to changes of 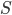 , e.g., consider set
, e.g., consider set 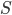 whose points are evenly distributed on the surface of a unit hypersphere, and let
whose points are evenly distributed on the surface of a unit hypersphere, and let 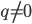 be a point arbitrarily close to the origin. The expansion constant of the set
be a point arbitrarily close to the origin. The expansion constant of the set  is
is 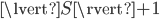 whereas the expansion constant of the set
whereas the expansion constant of the set  is
is 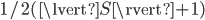 (this example was taken from the thesis Improving Dual-Tree Algorithms). With these bounds in mind and assuming the worst-case bounds on the cover tree algorithms are tight, we have to concede that these algorithms may require
(this example was taken from the thesis Improving Dual-Tree Algorithms). With these bounds in mind and assuming the worst-case bounds on the cover tree algorithms are tight, we have to concede that these algorithms may require 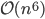 operations or worse. Even if the points are regularly spaced, the performance bounds may be bad. Consider a set
operations or worse. Even if the points are regularly spaced, the performance bounds may be bad. Consider a set 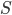 forming a
forming a 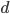 -dimensional hypercubic honeycomb, i.e., with
-dimensional hypercubic honeycomb, i.e., with 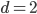 this is a regular square tiling. In this case, the expansion constant
this is a regular square tiling. In this case, the expansion constant  is proportional to
is proportional to 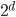 . Note that the expansion constant
. Note that the expansion constant  depends on the dimension of the subspace spanned by the points of
depends on the dimension of the subspace spanned by the points of 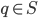 and not on the dimension of the space containing these points.
and not on the dimension of the space containing these points.
Nevertheless, cover trees are used in practice because real-world data sets often have small expansion constants. The expansion constant is related to the doubling dimension of a metric space (given a ball 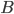 with unit radius in a
with unit radius in a 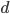 -dimensional metric space
-dimensional metric space 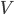 , the doubling dimension of
, the doubling dimension of 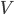 is the smallest number of balls with radius
is the smallest number of balls with radius 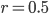 needed to cover
needed to cover 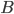 ).
).
Implementing Cover Trees
In a cover tree, given a point  on level
on level 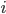 , there is a node for
, there is a node for  on all levels
on all levels 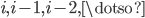 which raises the question how we can efficiently represent cover trees on a computer. Furthermore, we need to know if the number of levels in the cover tree can represented with standard integer types.
which raises the question how we can efficiently represent cover trees on a computer. Furthermore, we need to know if the number of levels in the cover tree can represented with standard integer types.
Given a point  that occurs on multiple levels in the tree, we can either
that occurs on multiple levels in the tree, we can either
- coalesce all nodes corresponding to
 and store the children in an associtive array whose values are child nodes and levels as keys, or
and store the children in an associtive array whose values are child nodes and levels as keys, or - we create one node corresponding to
 on each level whenever there are children, storing the level of the node as well as its children.
on each level whenever there are children, storing the level of the node as well as its children.
The memory consumption for the former representation can be calculated as follows: every cover tree node needs to store the corresponding point and the associative array. If the associative array is a binary tree, then for every level 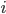 , there is one binary tree node with
, there is one binary tree node with
- a list of children of the cover tree node at level
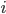 ,
, - a pointer to its left child,
- a pointer to its right child, and
- a pointer to the parent binary tree node so that we can implement iterators (this is how
std::mapnodes in the GCC C++ standard library are implemented).
Hence, for every level 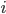 in the binary tree, we need to store at least four references and the level. The other representation must store the level, a reference to the corresponding point, and a reference to the list of children of this cover tree node so this representation is more economic with respect to the memory consumption. There is no difference in the complexity of nearest-neighbor searches because for an efficient nearest-neighbor search, we have to search the cover tree top down starting at the highest level.
in the binary tree, we need to store at least four references and the level. The other representation must store the level, a reference to the corresponding point, and a reference to the list of children of this cover tree node so this representation is more economic with respect to the memory consumption. There is no difference in the complexity of nearest-neighbor searches because for an efficient nearest-neighbor search, we have to search the cover tree top down starting at the highest level.
A metric maps its input to non-negative real values. On a computer (in finite precision arithmetic) there are bounds on the range of values that can be represented and we will elaborate on this fact using numbers in the IEEE-754 double-precision floating-point format as an example. An IEEE-754 float is a number 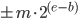 , where
, where 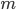 is called the mantissa (or significand),
is called the mantissa (or significand),  is called the exponent, and
is called the exponent, and  is a fixed number called bias. The sign bit of a double-precision float is represented with one bit, the exponent occupies 11 bits, the mantissa 52 bits, and the bias is
is a fixed number called bias. The sign bit of a double-precision float is represented with one bit, the exponent occupies 11 bits, the mantissa 52 bits, and the bias is 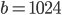 . The limited size of these two fields immediately bounds the number the quantities that can be represented and in fact, the largest finite double-precision float value is approximately
. The limited size of these two fields immediately bounds the number the quantities that can be represented and in fact, the largest finite double-precision float value is approximately 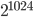 and the smallest positive value is
and the smallest positive value is 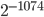 . Consequently, we will never need have more than
. Consequently, we will never need have more than 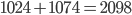 levels in a cover tree when using double-precision floats irrespective of the number of points stored in the tree. Thus, the levels can be represented with 16bit integers.
levels in a cover tree when using double-precision floats irrespective of the number of points stored in the tree. Thus, the levels can be represented with 16bit integers.
Existing Implementations
The authors of the original cover tree paper Cover Trees for Nearest Neighbors made their C and C++ implementations available on the website http://hunch.net/~jl/projects/cover_tree/cover_tree.html. The first author of the paper Faster Cover Trees made the Haskell implementation of a nearest ancestor cover tree used for this paper available on GitHub. The C++ implementation by Manzil Zaheer features  -nearest neighbor search, range search, and parallel construction based on C++ concurrency features (GitHub). The C++ implementation by David Crane can be found in his repository on GitHub. Note that the worst-case complexity of node removal is linear in this implementation because of a conspicuous linear vector search. The most well maintained implementation of a cover tree can probably be found in the MLPACK library (also C++). I implemented a nearest ancestor cover tree in C++14 which takes longer to construct but has superior performance during nearest neighbor searches. The code can be found in my git repository.
-nearest neighbor search, range search, and parallel construction based on C++ concurrency features (GitHub). The C++ implementation by David Crane can be found in his repository on GitHub. Note that the worst-case complexity of node removal is linear in this implementation because of a conspicuous linear vector search. The most well maintained implementation of a cover tree can probably be found in the MLPACK library (also C++). I implemented a nearest ancestor cover tree in C++14 which takes longer to construct but has superior performance during nearest neighbor searches. The code can be found in my git repository.
Numerical Experiments
The worst-case complexity bounds of common cover tree operations, e.g., construction and querying, contain terms 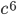 or
or 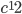 , where
, where  is the expansion constant. In this section, I will measure the effect of the expansion constant on the run-time of batch construction and nearest-neighbor search on a synthetic data set.
is the expansion constant. In this section, I will measure the effect of the expansion constant on the run-time of batch construction and nearest-neighbor search on a synthetic data set.
For the experiment, I implemented a nearest ancestor cover tree described in Faster Cover Trees in C++14 with batch construction, nearest-neighbor search (single-tree algorithm), and without associative arrays. The first point in the data set is chosen as the root of the cover tree and on every level of the cover tree, the construction algorithm attempts to select the points farthest away from the root as children.
The data consists of random points in 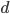 -dimensional space with uniformly distributed entries in the interval
-dimensional space with uniformly distributed entries in the interval 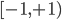 , i.e., we use random points inside of a hypercube. The reference set (the cover tree) contains
, i.e., we use random points inside of a hypercube. The reference set (the cover tree) contains 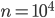 points and we performed nearest-neighbor searches for
points and we performed nearest-neighbor searches for 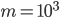 random points. The experiments are conducted using the Manhattan, the Euclidean, and the Chebychev metric and the measurements were repeated 25 times for dimensions
random points. The experiments are conducted using the Manhattan, the Euclidean, and the Chebychev metric and the measurements were repeated 25 times for dimensions 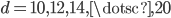 .
.
We do not attempt to measure the expansion constant for every set of points. Instead, we approximate the expansion constant from the dimension 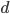 . Let
. Let 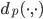 ,
, 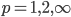 , be a metric, where
, be a metric, where
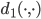 is the Manhattan metric,
is the Manhattan metric,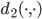 is the Euclidean metric, and
is the Euclidean metric, and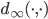 is the Chebychev metric,
is the Chebychev metric,
and let 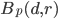 be the ball centered at the origin with radius
be the ball centered at the origin with radius 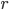 :
:

The expansion constant  of a set
of a set 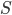 was defined as the smallest scalar
was defined as the smallest scalar 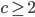 such that
such that
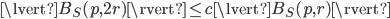
for all  ,
, 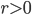 . We will now simplify both sides of the inequality.
. We will now simplify both sides of the inequality.
In this experiment, all entries of the points are uniformly distributed around the origin and using the assumption that 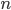 and
and 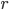 are sufficiently large,
are sufficiently large, 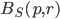 will be approximately constant everywhere in the hypercube containing the points:
will be approximately constant everywhere in the hypercube containing the points:
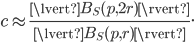
Using the uniform distribution property again, we can set 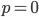 without loss of generality. Likewise, since
without loss of generality. Likewise, since 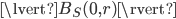 is approximately constant, the fraction above will be close to the ratio of the volumes of the balls
is approximately constant, the fraction above will be close to the ratio of the volumes of the balls 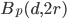 and
and 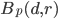 .
. 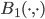 is called a cross-polytope and its volume can be computed with
is called a cross-polytope and its volume can be computed with
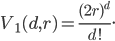
The volume of the 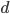 -ball in Euclidean space
-ball in Euclidean space 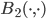 is
is
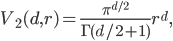
where 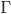 is the gamma function. Finally,
is the gamma function. Finally, 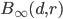 is a hypercube with volume
is a hypercube with volume
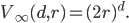
Using our assumptions, it holds that
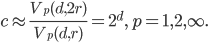
Consequently, the worst-case bounds are 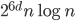 for construction and
for construction and 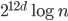 for nearest-neighbor searches in cover trees with this data set.
for nearest-neighbor searches in cover trees with this data set.
In the plots, 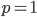 indicates the Manhattan,
indicates the Manhattan, 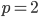 the Euclidean, and
the Euclidean, and 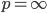 the Chebychev metric with the markers corresponding to the shape of the Ball
the Chebychev metric with the markers corresponding to the shape of the Ball 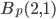 .
.
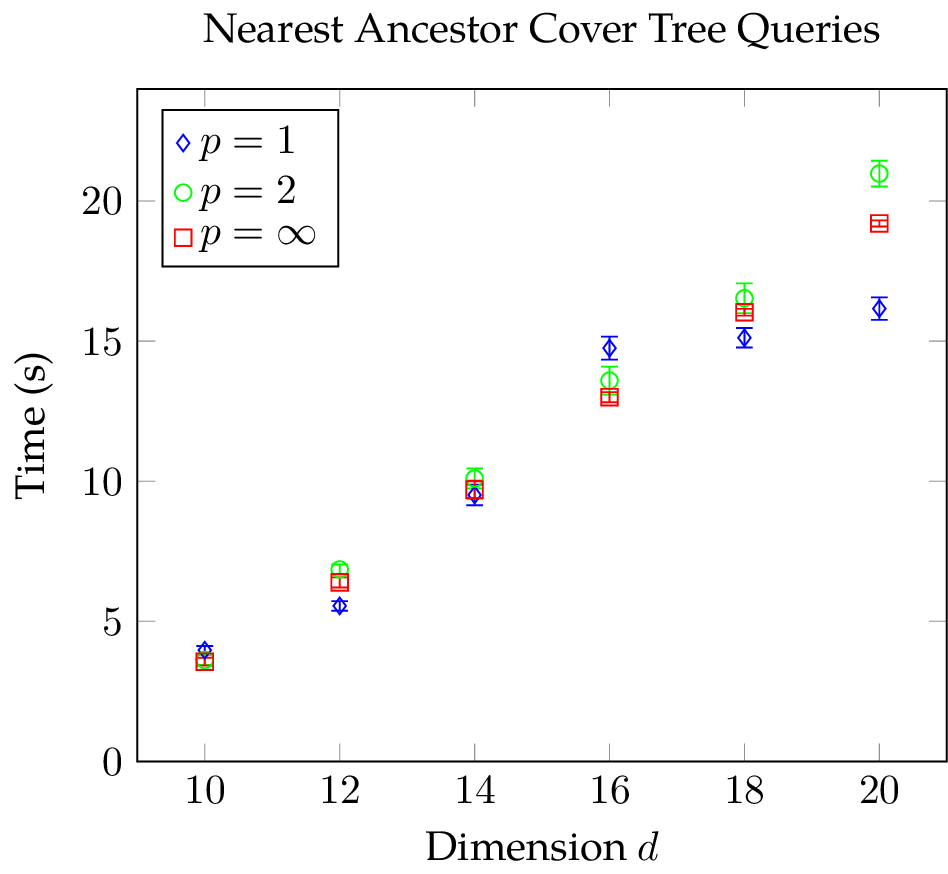
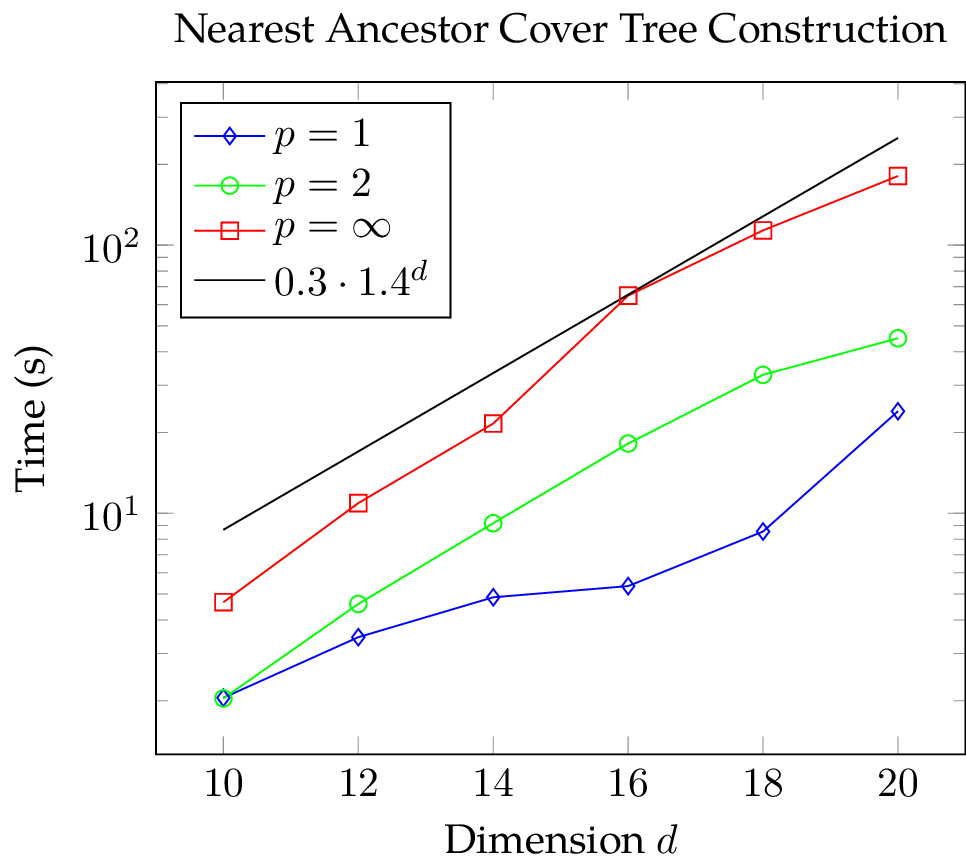
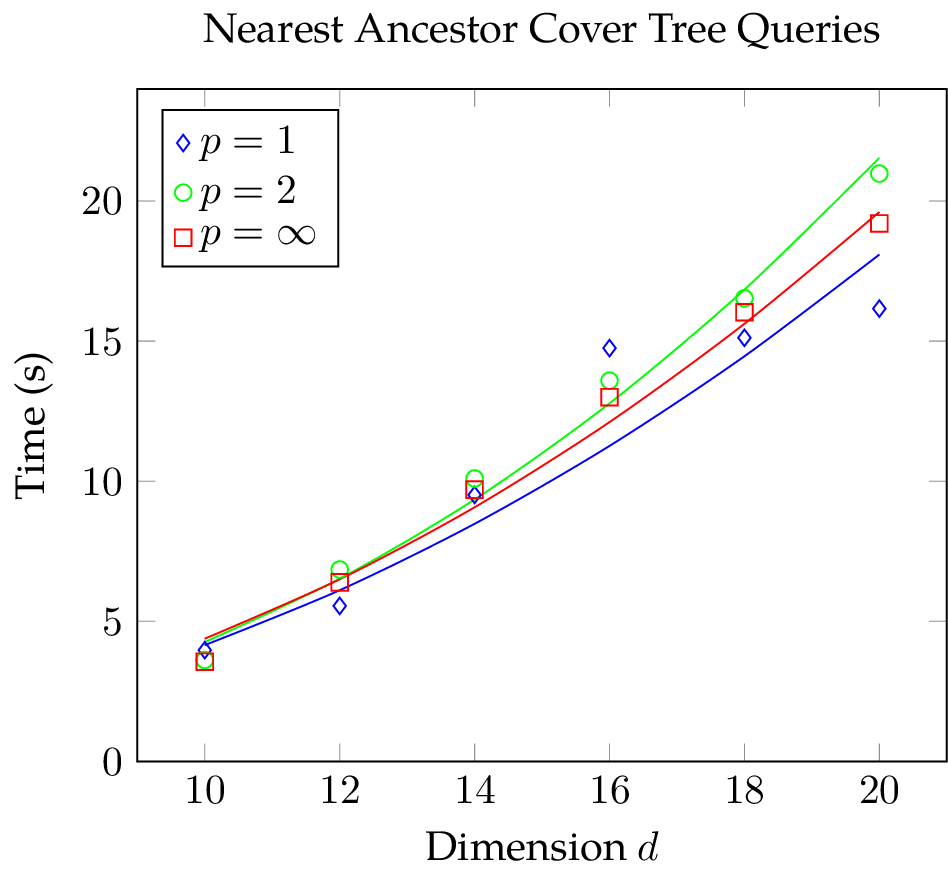
The figures below show mean and standard deviation for construction and query phase. The construction time of the cover tree is strongly dependent on the used metric: cover tree construction using the Chebychev metric takes considerably more time than with the other norms; construction with the Manhattan metric is slightly faster than with the Euclidean metric. Observe that there is a large variation in the construction time when employing the Euclidean metric and this effect becomes more pronounced the higher the dimension 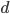 . Also, considering the small standard deviation in the data, the construction time slightly jumps at
. Also, considering the small standard deviation in the data, the construction time slightly jumps at 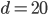 for the Manhattan norm. In the query time plot, we can see that the results are mostly independent of the metric at hand. What is more, the variance of the query time is without exception small in comparison to the mean. Nevertheless, there is a conspicuous bend at
for the Manhattan norm. In the query time plot, we can see that the results are mostly independent of the metric at hand. What is more, the variance of the query time is without exception small in comparison to the mean. Nevertheless, there is a conspicuous bend at 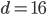 when using the Manhattan metric. This bend is unlikely to be a random variation because we repeated the measurements 25 times and the variance is small.
when using the Manhattan metric. This bend is unlikely to be a random variation because we repeated the measurements 25 times and the variance is small.
With our measurements we want to determine how the expansion constant influences construction and query time and according to the estimates above, we ought to see an exponential growth in operations. To determine if the data points could have been generated by an exponential function, one can plot the data with a logarithmic scaling along the vertical axis. Then, exponential functions will appear linear and polynomials sub-linear. In the figures below, we added an exponential function for comparison and it seems that the construction time does indeed grow exponentially with the dimension 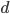 irrespective of the metric at hand while the query time does not increase exponentially with the dimension.
irrespective of the metric at hand while the query time does not increase exponentially with the dimension.
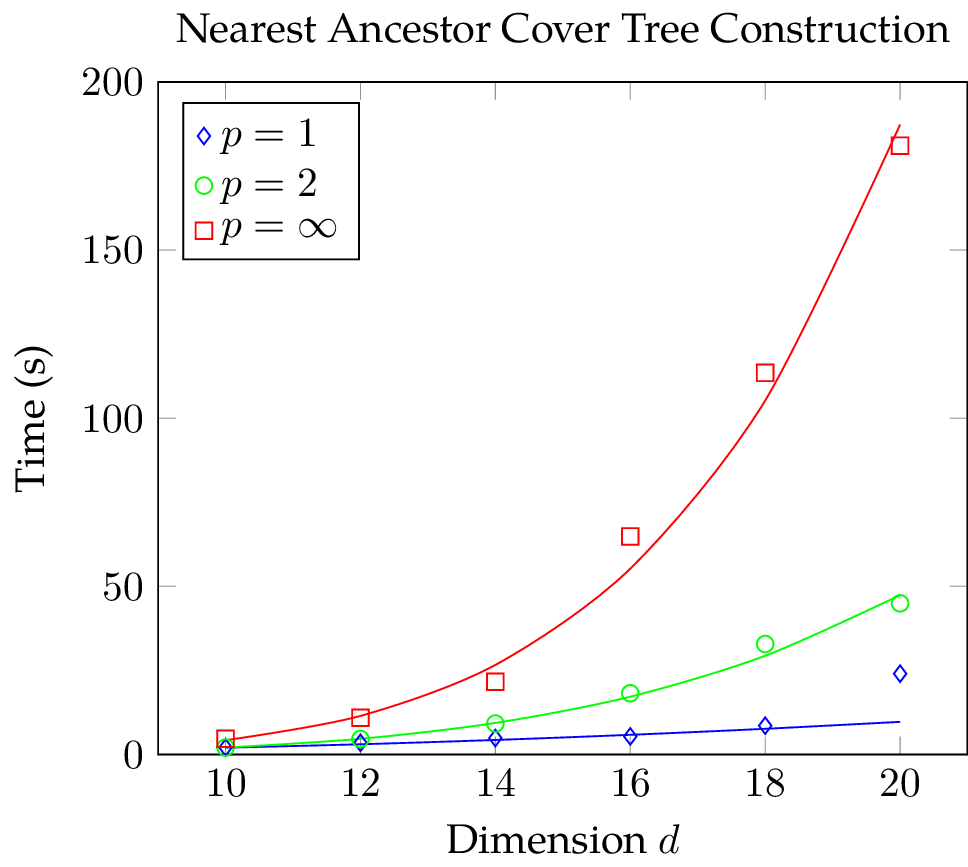
Seeing the logarithmic plots, I attempted to fit an exponential function 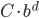 ,
, 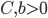 , to the construction time data. The fitted exponential did not approximate the data of the Euclidean and Manhattan metric well even when considering the standard deviation. However, the fit for the Chebychev metric was very good. In the face of these results, I decided to fit a monomial
, to the construction time data. The fitted exponential did not approximate the data of the Euclidean and Manhattan metric well even when considering the standard deviation. However, the fit for the Chebychev metric was very good. In the face of these results, I decided to fit a monomial 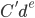 ,
, 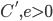 , to both construction and query time data and the results can be seen below. Except for the Manhattan metric data, the fit is very good.
, to both construction and query time data and the results can be seen below. Except for the Manhattan metric data, the fit is very good.
The value of the constants are for construction:
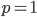 :
: 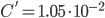 ,
, 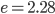 ,
,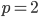 :
: 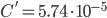 ,
, 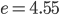 ,
,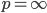 :
: 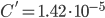 ,
, 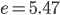 .
.
For nearest-neighbor searches, the constants are
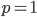 :
: 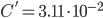 ,
, 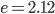 ,
,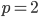 :
: 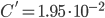 ,
, 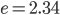 ,
,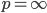 :
: 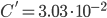 ,
, 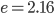 .
.
In conclusion, for our test data the construction time of a nearest ancestor cover tree is strongly dependent on the metric at the hand and the dimension of the underlying space whereas the query time is mostly indepedent of the metric and a function of the square of the dimension 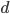 . The jumps in the data of the Manhattan metric and the increase in variation in the construction time when using the Euclidean metric highlight that there must be non-trivial interactions between dimension, metric, and the cover tree implementation.
. The jumps in the data of the Manhattan metric and the increase in variation in the construction time when using the Euclidean metric highlight that there must be non-trivial interactions between dimension, metric, and the cover tree implementation.
Originally, we asked how the expansion constant  impacts the run-time of cover tree operations and determined that we can approximate
impacts the run-time of cover tree operations and determined that we can approximate  by calculating
by calculating 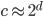 . Thus, the run-time
. Thus, the run-time 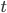 of construction and nearest-neighbor search seems to be proportional to
of construction and nearest-neighbor search seems to be proportional to 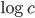 because
because 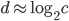 and
and 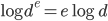 .
.
Conclusion
We introduced cover trees, discussed their advantages as well as their unique theoretical properties. We elaborated on the complexity of cover tree operations, the expansion constant, and implementation aspects. Finally, we conducted an experiment on a synthetic data set and found that the construction time is strongly dependent on the metric and the dimension 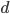 of the underlying space while the time needed for nearest-neighbor search is almost independent of the metric. Most importantly, the complexity of operations seems to be polynomial in
of the underlying space while the time needed for nearest-neighbor search is almost independent of the metric. Most importantly, the complexity of operations seems to be polynomial in 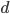 and proportional to the logarithm of the expansion constant. There are unexplained jumps in the measurements.
and proportional to the logarithm of the expansion constant. There are unexplained jumps in the measurements.