RANLUX denotes a class of high-quality pseudo-random number generators (PRNGs) with long periods, solid theoretical foundations, and uses in computational physics. These generators are built on top of add-with-carry and subtract-with-borrow PRNGs which allow customization through three user-provided parameters yet there are only two variants in use today working internally with 24-bit and 48-bit arithmetic; this comes at a cost because modern computers do not possess instructions for 24-bit or 48-bit arithmetic. In this blog post I will present the theory behind RANLUX PRNGs, a list of possible parameters for 16-, 32-, and 64-bit RANLUX generators, criteria for selecting generators as well as benchmarks comparing the most competitive RANLUX variants with the RANLUX generators in the C++11 standard library, the Mersenne Twister, and xoshiro128+.
Some of the new RANLUX flavors are easily implemented in C++11 (sometimes in only two lines of code), they are faster than the existing RANLUX flavors, they retain all desirable properties of a RANLUX generator, and they pass all DieHarder and TestU01 BigCrush PRNG tests.
The programs used to compute the RANLUX parameters are called ranlux-tools. They are free software under the terms of the Mozilla Public License 2.0 and can be found online:
https://christoph-conrads.name/software/ranlux-tools
Introduction
RANLUX PRNGs are built on top of add-with-carry (AWC) and subtract-with-borrow generators (SWB). They arise from the same mathematical principles so from now on, I will call them AWC/SWB PRNGs. As of the time of writing of this blog post, the class of AWC/SWB generators were introduced in a paper by George Marsaglia and Arif Zaman almost thirty years ago. These PRNGs can be customized with three parameters  ,
, 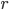 , and
, and 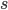 , the generators draw uniformly-distributed random integer values in the interval
, the generators draw uniformly-distributed random integer values in the interval 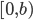 with periods of length up to
with periods of length up to 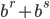 . A major challenge with respect to the choice of parameters lies in the integer factorization of numbers of the form
. A major challenge with respect to the choice of parameters lies in the integer factorization of numbers of the form 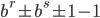 during the calculation of the period length; the signs depend on the flavor of AWC/SWB generator at hand. The article by Marsaglia and Zaman provided only a few parameter choices for
during the calculation of the period length; the signs depend on the flavor of AWC/SWB generator at hand. The article by Marsaglia and Zaman provided only a few parameter choices for 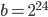 and
and 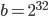 for SWB generators because of a lack of computational resources at the time. They state this clearly in the last paragraph of their paper. For reasons unknown to me, generator variants with
for SWB generators because of a lack of computational resources at the time. They state this clearly in the last paragraph of their paper. For reasons unknown to me, generator variants with 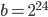 and
and 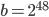 remain the only ones available in software libraries, e.g., the C++11 standard library, the GNU Scientific Library, and Boost.Random in the Boost C++ Libraries incorporate such a generator. Using almost thirty years of progress in computer hardware and integer factorization, I will revisit the the parameter choices and propose new parameters for bases
remain the only ones available in software libraries, e.g., the C++11 standard library, the GNU Scientific Library, and Boost.Random in the Boost C++ Libraries incorporate such a generator. Using almost thirty years of progress in computer hardware and integer factorization, I will revisit the the parameter choices and propose new parameters for bases  that match register sizes on common instruction set architectures (ISA) like x86-64 or ARMv7-A.
that match register sizes on common instruction set architectures (ISA) like x86-64 or ARMv7-A.
Initially I will introduce AWC/SWB PRNGs and discuss parameter constraints ensuring long periods. Based on this, I will present a selection of possible parameters for 16-, 32-, and 64-bit AWCs and SWBs generators. AWC/SWB PRNG on their own fail simple empirical PRNG tests. For this reason we will discuss these generators from the dynamical systems point of view leading us to generously discarding values drawn from AWC/SWB random number engines. This step marks the difference between plain AWCs/SWBs and RANLUX generators. Afterwards, I will present possible RANLUX parameter choices for 16-, 32-, and 64-bit RANLUX generators.
Depending on the AWC/SWB parameter choices, one must sometimes discard up to 95% of the generator values making RANLUX PRNGs significantly slower than other designs. In the the section on implementation aspects, I will attempt to narrow the speed gap by using RANLUX generators where one has to discard less values and by optimizing their implementation. The most desirable RANLUX flavors were implemented by me in C++11 which allows me to show benchmark results comparing 24-bit RANLUX, the new RANLUX modifications, the Mersenne Twister, and xoshiro128+.
Benchmarks can be found throughout this blog post. All tested PRNGs are implemented in C++11. Therefore the performance of the each PRNG depends on the instruction set architecture, the compiler, the compiler version, and the C++ standard library implementation. Unfortunately, the performance also varies significantly. To restrict the number of experiments to perform this blog post will use only GCC 8.2.0 on x86-64 as well as Clang 3.5.0 on ARMv7-A (a Raspberry Pi 3B). The compiler flags are -DNDEBUG -O3 -march=native. The experiments will exclusively use the GNU C++ Library (libstdc++) because libc++ consumes decidedly more CPU time for the same tasks on both platforms. Note that on x86-64, GCC 8.2.0 generates optimized code for the C++11 standard library class std::subtract_with_carry_engine that is about twice as fast as the same code compiled with GCC 7.3.0 or Clang 6.0.1; my code also benefits from optimization passes specific to GCC 8.2.0 but to a much smaller degree. The benchmarks always measure the time to generate one billion random values and the compilers are barred from inlining the calls to the random number engines to suppress unrealistic compiler optimizations. Nevertheless, the benchmarks are purely synthetic and the call overhead is decreasing the relative performance difference between the different generators. The code for the benchmarks can be found in the ranlux-tools. On the Raspberry Pi the C99 function clock() gave wrong results; clock_gettime() is called directly instead.
Add-With-Carry and Subtract-With-Borrow PRNGs
Introduction and Theory
George Marsaglia and Arif Zaman introduced four flavors of Lagged Fibonacci PRNGs in their 1991 paper A New Class of Random Number Generators. Given integers 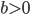 ,
, 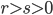 , the generated values
, the generated values 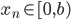 are computed with the recurrences in the list below (the significance of the variable $m$ will be explained further down):
are computed with the recurrences in the list below (the significance of the variable $m$ will be explained further down):
- Method 1
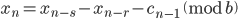
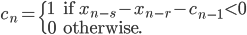
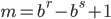
- Method 2
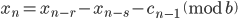
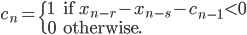
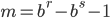
- Method 3
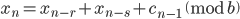
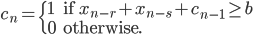
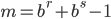
- Method 4
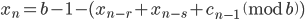
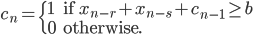
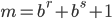
where 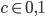 is a carry bit,
is a carry bit,  is called base,
is called base, 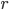 is called long lag,
is called long lag, 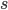 is called short lag, and
is called short lag, and 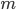 is called modulus. Observe when
is called modulus. Observe when  matches the word size of the computer, then
matches the word size of the computer, then 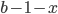 is the bit-wise complement of
is the bit-wise complement of 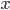 . Method I and II are called subtract-with-borrow generators (SWB), method III is called an add-with-carry generator (AWC), and method IV is a complementary AWC generator (CAWC). Below I may write
. Method I and II are called subtract-with-borrow generators (SWB), method III is called an add-with-carry generator (AWC), and method IV is a complementary AWC generator (CAWC). Below I may write
- SWB(b, s, r) for Method I generators,
- SWB(b, r, s) for Method II generators, and
- AWC(b, r, s) for Method III generators.
There is no notation for CAWC because I did not find any parameter combinations for native integer types. To keep the text succinct, I may write "an AWC" or "an SWB" when I mean an AWC or an SWB PRNG, respectively. The significance of the modulus will be discussed later in a dedicated section.
The 24-bit RANLUX PRNG in use nowadays uses 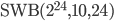 internally, 48-bit RANLUX is based on
internally, 48-bit RANLUX is based on 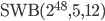 . In the remainder of the text, we will call these two RANLUX PRNGs that are currently implemented in many software libraries 24-bit RANLUX and 48-bit RANLUX, respectively, even though there are many RANLUX generators with base
. In the remainder of the text, we will call these two RANLUX PRNGs that are currently implemented in many software libraries 24-bit RANLUX and 48-bit RANLUX, respectively, even though there are many RANLUX generators with base 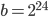 and
and 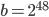 .
.
The variates 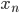 of AWCs and SWBs are provably uniformly distributed over the full period(!) and can be expected to possess periods as long as other PRNGs with same amount of state: Many generators with
of AWCs and SWBs are provably uniformly distributed over the full period(!) and can be expected to possess periods as long as other PRNGs with same amount of state: Many generators with 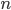 bits of state have period lengths of about
bits of state have period lengths of about 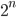 and this holds approximately also for AWC and SWBs. For example
and this holds approximately also for AWC and SWBs. For example 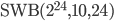 has
has 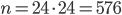 bits of state (plus the carry bit) and period
bits of state (plus the carry bit) and period 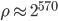 .
.
Choice of Base and Its Effect on Speed
This idea behind this blog post was originally that currently implemented RANLUX variants do not use CPU-native arithmetic internally; this property should incur a performance penalty. For this reason, I will measure the performance of 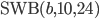 as a function of the base
as a function of the base  . As a reminder, the benchmark setup for all experiments in this blog post was explained at the end of the introduction.
. As a reminder, the benchmark setup for all experiments in this blog post was explained at the end of the introduction.
The first column shows the PRNG, the second column shows the time until a fixed number of samples was computed relative to 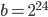 (i.e., lower is faster), and the third column shows the throughput relative to the PRNG with
(i.e., lower is faster), and the third column shows the throughput relative to the PRNG with 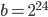 (i.e., the higher the value, the higher the throughput). The bases
(i.e., the higher the value, the higher the throughput). The bases  used in the experiment were
used in the experiment were 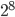 ,
, 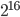 ,
, 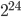 ,
, 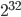 , and
, and 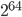 . On x86-64 base
. On x86-64 base 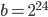 yields the slowest generator by far and its throughput is second-to-last. On ARMv7-A, base
yields the slowest generator by far and its throughput is second-to-last. On ARMv7-A, base 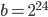 results in a faster SWB than b=
results in a faster SWB than b=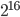 and
and 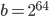 . Also, the larger the base
. Also, the larger the base  , the larger the throughput. In summary, the choice
, the larger the throughput. In summary, the choice 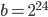 has a disastrous effect on performance on x86-64 in this experiment but no particular effect on ARMv7-A with Clang 3.5.0. Moreover, the native word size (
has a disastrous effect on performance on x86-64 in this experiment but no particular effect on ARMv7-A with Clang 3.5.0. Moreover, the native word size (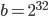 on ARMv7-A,
on ARMv7-A, 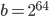 on x86-64) on both instruction set architectures (ISAs) yields the PRNG with both the highest speed and the highest throughput. Finally,
on x86-64) on both instruction set architectures (ISAs) yields the PRNG with both the highest speed and the highest throughput. Finally, 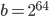 yields the highest throughput on both platforms. The question behind this experiment was if 24-bit arithmetic incurs a performance penalty; there is a performance penalty in comparison to the native integer type of the platform.
yields the highest throughput on both platforms. The question behind this experiment was if 24-bit arithmetic incurs a performance penalty; there is a performance penalty in comparison to the native integer type of the platform.
| Generator | ARMv7-A CPU time | ARMv7-A Throughput | x86-64 CPU time | x86-64 Throughput |
|---|---|---|---|---|
| SWB(2^8, 10, 24) | 0.96 | 0.35 | 0.65 | 0.52 |
| SWB(2^16, 10, 24) | 1.15 | 0.58 | 0.54 | 1.24 |
| SWB(2^24, 10, 24) | 1.00 | 1.00 | 1.00 | 1.00 |
| SWB(2^32, 10, 24) | 0.96 | 1.38 | 0.54 | 2.47 |
| SWB(2^64, 10, 24) | 1.44 | 1.85 | 0.52 | 5.13 |
Computing Period Lengths
When I introduced the PRNGs by Marsaglia and Zaman, I showed a list with the recurrences; this list also contained the variable 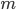 for each generator whose significance was not explained. To ensure an AWC/SWB period of maximum length,
for each generator whose significance was not explained. To ensure an AWC/SWB period of maximum length, 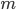 must be a prime number and
must be a prime number and  must be a primitive root modulo
must be a primitive root modulo 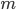 , i.e., for every integer
, i.e., for every integer 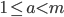 , there is a positive integer exponent
, there is a positive integer exponent 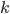 such that
such that 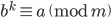 . Since I want to use specific word sizes on modern computers,
. Since I want to use specific word sizes on modern computers,  will be a power of two in this article and then
will be a power of two in this article and then  might not be a primitive root. Nevertheless, the period is usually still long but not at maximum. The remainder of this section explains how to compute the period length.
might not be a primitive root. Nevertheless, the period is usually still long but not at maximum. The remainder of this section explains how to compute the period length.
The period length of an AWC/SWB equals the multiplicative order of  modulo
modulo 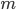 . The multiplicative order
. The multiplicative order 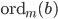 is the smallest integer
is the smallest integer 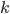 such that
such that 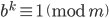 and if
and if  is a primitive root modulo
is a primitive root modulo 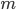 , then
, then 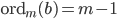 . Hagen von Eitzen outlined a method for the computation of the multiplicative order in a Stack Exchange post. The algorithm takes advantage of modular arithmetic and Fermat's little theorem which says that if
. Hagen von Eitzen outlined a method for the computation of the multiplicative order in a Stack Exchange post. The algorithm takes advantage of modular arithmetic and Fermat's little theorem which says that if  is any prime number and
is any prime number and 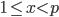 an integer, then
an integer, then 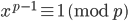 . Hence, we know that
. Hence, we know that 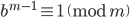 because the modulus
because the modulus 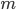 is prime but we do not know if
is prime but we do not know if 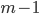 is the smallest integer with this property. In modular arithmetic it holds that if
is the smallest integer with this property. In modular arithmetic it holds that if 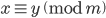 , then
, then 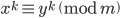 for any natural number
for any natural number 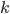 . This tells us that
. This tells us that 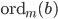 must be a (composite) factor of
must be a (composite) factor of 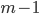 . von Eitzen's algorithm exploits this property by systematically testing the prime factors of
. von Eitzen's algorithm exploits this property by systematically testing the prime factors of 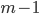 . Specifically, let
. Specifically, let  be a prime factor of
be a prime factor of 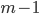 . If
. If 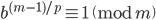 , then
, then  cannot be a factor of
cannot be a factor of 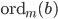 . If
. If 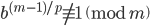 , then
, then  must be a factor of
must be a factor of 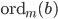 . Repeating this procedure for all prime factors of
. Repeating this procedure for all prime factors of 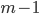 will then yield all prime factors of
will then yield all prime factors of 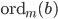 .
.
Let 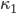 be an integer such that
be an integer such that 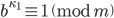 and let
and let 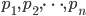 be prime factors of
be prime factors of 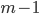 . For every factor
. For every factor 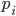 ,
, 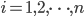 , compute
, compute 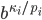 . If the result is congruent to one modulo
. If the result is congruent to one modulo 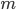 , then set
, then set 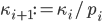 ,
, 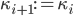 otherwise. At the end of the algorithm, the period length will be stored in
otherwise. At the end of the algorithm, the period length will be stored in 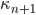 . Since
. Since 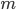 is prime, Fermat's little theorem allows us to set
is prime, Fermat's little theorem allows us to set 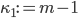 .
.
Integer factorization is a hard problem and certain parameter choices give rise to moduli with more than thousand bits, e.g., the modulus of 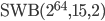 already has 963 bits. Depending on the factorization method (e.g., the Elliptic Curve Method) the computational complexity depends only on the number of digits of a desired prime factor but I was still unable to completely factorize some integers
already has 963 bits. Depending on the factorization method (e.g., the Elliptic Curve Method) the computational complexity depends only on the number of digits of a desired prime factor but I was still unable to completely factorize some integers 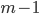 . Yet if the algorithm above is correct, then this is not an insurmountable problem. Reconsider the algorithm above but without the requirement that
. Yet if the algorithm above is correct, then this is not an insurmountable problem. Reconsider the algorithm above but without the requirement that 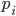 is prime. If
is prime. If 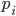 is prime, then apply the rules from above. If
is prime, then apply the rules from above. If 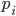 is not prime and if
is not prime and if 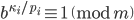 , then set
, then set 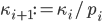 as above because
as above because 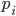 cannot be a factor of
cannot be a factor of 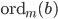 . If
. If 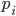 is not prime and if
is not prime and if 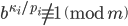 , then
, then 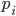 must have factors in common with
must have factors in common with 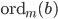 . In this case setting
. In this case setting 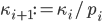 yields a lower bound for
yields a lower bound for 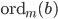 and setting
and setting 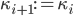 gives an upper bound. This lower bound may actually be sufficiently large for practical applications.
gives an upper bound. This lower bound may actually be sufficiently large for practical applications.
The values 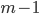 were factorized with the aid of the Python2 module primefac as well as the programs GMP-ECM and Cado-NFS. The prime factors were then used by a Python implementation of the algorithm above; it found in the ranlux-tools repository. The computed cycle lengths match the numbers in the Marsaglia/Zaman paper in Section 6.2. Note that Table 2 in their paper should show the same values but it seems the table headings are not matching the column content.
were factorized with the aid of the Python2 module primefac as well as the programs GMP-ECM and Cado-NFS. The prime factors were then used by a Python implementation of the algorithm above; it found in the ranlux-tools repository. The computed cycle lengths match the numbers in the Marsaglia/Zaman paper in Section 6.2. Note that Table 2 in their paper should show the same values but it seems the table headings are not matching the column content.
RANLUX PRNGs
Introduction and Theory
AWC and SWB generate provably uniformly distributed values over the full period but they also possess an easily discernible lattice structure, they do not pass common empirical RNG tests, e.g., the Gap test, and they lead to inaccurate results in physics simulations involving the Monte Carlo method and Ising models, see for example the articles The Wheel of Fortune and On the Lattice Structure of the Add-With-Carry and Subtract-With-Borrow Random Number Generators. Martin Lüscher analysed this shortcoming in the paper A Portable High-Quality Random Number Generator for Lattice Field Theory Simulations.
Let 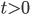 be a natural number, let
be a natural number, let 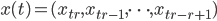 be a vector containing the state of an AWC/SWB, let
be a vector containing the state of an AWC/SWB, let 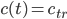 . Observe that one can compute the next generator state
. Observe that one can compute the next generator state 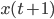 ,
, 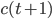 only by considering
only by considering 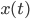 and
and 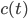 . We can also think of
. We can also think of 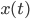 as a vector in
as a vector in 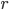 -dimensional space. In fact,
-dimensional space. In fact, 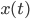 lies is inside an
lies is inside an 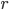 -dimensional hypercube with edge length
-dimensional hypercube with edge length  . Let
. Let
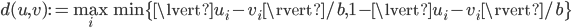
denote the distance between two points 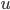 ,
, 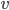 inside the hypercube, let
inside the hypercube, let 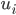 ,
, 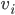 be
be 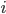 -th entries of these vectors. If
-th entries of these vectors. If 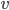 is a random vector, then the expected value of
is a random vector, then the expected value of 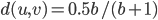 for all vectors
for all vectors 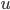 in the hypercube. Let
in the hypercube. Let 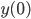 be a vector inside the hypercube with
be a vector inside the hypercube with 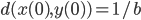 . Lüscher subjected the AWCs/SWBs to an analysis from the dynamical system point of view and his insight was that
. Lüscher subjected the AWCs/SWBs to an analysis from the dynamical system point of view and his insight was that 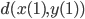 would be close to each other implying a decidedly non-random behavior. Based on this observation, he concluded there is a necessity to discard PRNG values until the expected value of
would be close to each other implying a decidedly non-random behavior. Based on this observation, he concluded there is a necessity to discard PRNG values until the expected value of 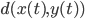 is
is 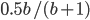 .
.
In this blog post, I will call smallest integer 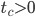 with average distance
with average distance 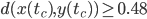 the time to chaos. Considering that RANLUX can use only
the time to chaos. Considering that RANLUX can use only 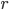 out of every
out of every 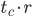 values drawn from an AWC/SWB if one requires truly uniformly distributed variates, the time the chaos is the second important factor in PRNG performance apart from the raw AWC/SWB speed.
values drawn from an AWC/SWB if one requires truly uniformly distributed variates, the time the chaos is the second important factor in PRNG performance apart from the raw AWC/SWB speed.
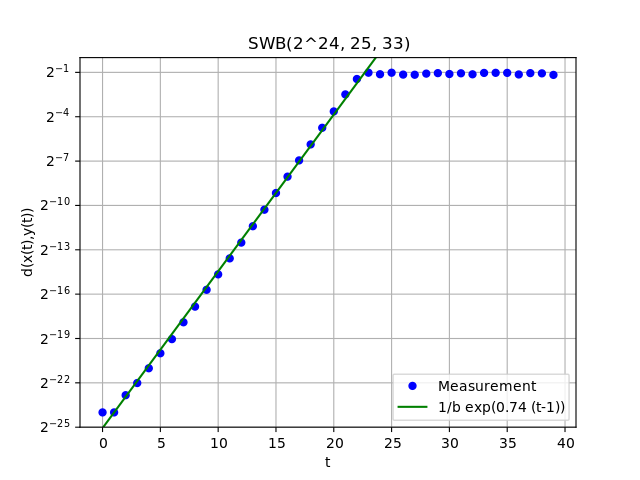
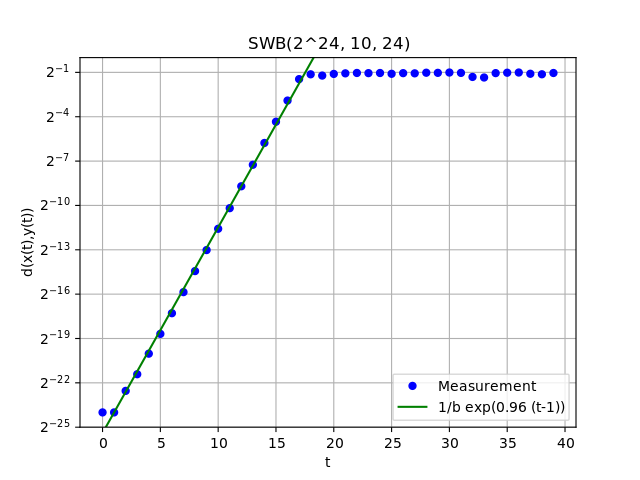
Based on mathematical considerations, Lüscher showed experimentally for 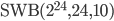 that the expected distance between two vectors with initial distance
that the expected distance between two vectors with initial distance 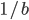 in the hypercube grows exponentially as a function of
in the hypercube grows exponentially as a function of 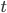 by fitting a function of the form
by fitting a function of the form 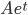 ,
, 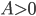 , to the data (this is equivalent to
, to the data (this is equivalent to 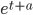 where
where 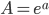 ). I can reproduce this result for this parameter combination. In general though, the ansatz function
). I can reproduce this result for this parameter combination. In general though, the ansatz function 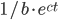 provides the best fit (i.e., an exponential function with base
provides the best fit (i.e., an exponential function with base 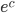 ) and this is demonstrated in the plots below. There, one can see the the average distance between
) and this is demonstrated in the plots below. There, one can see the the average distance between 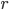 -dimensional vectors as a function of
-dimensional vectors as a function of 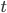 . The initial vectors
. The initial vectors 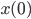 ,
, 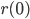 have distance
have distance 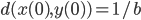 .
.
For the selection of AWCs and SWBs, there should be an unambiguous way to determine the time to chaos 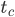 . Here, the following procedure was used to compute the time to chaos for a given PRNG:
. Here, the following procedure was used to compute the time to chaos for a given PRNG:
- Use the given PRNG and compute a random starting vector
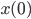 in the hypercube above.
in the hypercube above. - Create a random vector
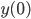 with distance
with distance 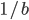 to
to 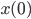 .
. - Compute
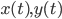 ,
, 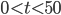 , and store the values
, and store the values 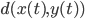 .
. - Repeat the previous steps 1,000 times and average the computed distances.
- Determine
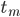 , the smallest value of
, the smallest value of 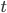 such that the average distance is above
such that the average distance is above 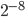 .
. - Fit a function
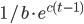 with least squares regression to the measured average distances for
with least squares regression to the measured average distances for 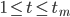 .
. - Determine the time to chaos: find the smallest integer
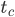 such that
such that 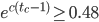 .
.
Searching for RANLUX Parameters
This section will explain the search criteria employed in ranlux-tools before showing a small selection of possible parameter combinations. Only the most relevant parameters can be found in this table because there are at least thirty possible combinations for 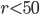 for each AWC and SWB. Moreover, I was unable to factorize many integers
for each AWC and SWB. Moreover, I was unable to factorize many integers 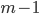 leaving me without information about the period length and causing a lot of blanks in the table. In my opinion, only the combination of the provably good randomness with a verifiable long period makes RANLUX generators desirable. The scripts in ranlux-tools can compute all possible parameter combinations for all values for
leaving me without information about the period length and causing a lot of blanks in the table. In my opinion, only the combination of the provably good randomness with a verifiable long period makes RANLUX generators desirable. The scripts in ranlux-tools can compute all possible parameter combinations for all values for 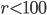 and bases
and bases  with powers of two at most
with powers of two at most 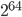 within 20 minutes on a reasonably recent x86-64 CPU.
within 20 minutes on a reasonably recent x86-64 CPU.
In general, the scripts in ranlux-tool searched for bases 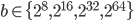 for values
for values 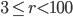 . Moreover, the short lag
. Moreover, the short lag 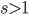 must not be a divisor of the long lag (
must not be a divisor of the long lag (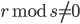 ) to avoid short cycles. To add to that, the table does not contain entries where two is a common divisor of the short lag and the long lag since these parameter combinations would appear again in the table for base
) to avoid short cycles. To add to that, the table does not contain entries where two is a common divisor of the short lag and the long lag since these parameter combinations would appear again in the table for base 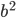 with double the time to chaos. I also constrained the parameter search such that
with double the time to chaos. I also constrained the parameter search such that 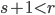 if
if 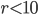 ,
, 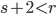 if
if 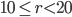 and
and 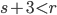 otherwise.
otherwise.
The table below shows the AWC/SWB type, the base  , the long lag
, the long lag 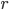 , the short lag
, the short lag 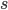 , the time to chaos
, the time to chaos 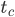 , and the base 2 logarithm of the period length
, and the base 2 logarithm of the period length 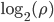 ; the values in the last columns have been rounded down. I did not find any CAWC combinations with the given bases.
; the values in the last columns have been rounded down. I did not find any CAWC combinations with the given bases. 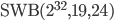 from Table 2 in the Marsaglia/Zaman paper is missing because its modulus
from Table 2 in the Marsaglia/Zaman paper is missing because its modulus 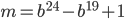 is not prime according to
is not prime according to openssl prime. This fact can also be verified with Fermat's little theorem. The table also contains an entry for 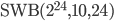 , the SWB inside 24-bit RANLUX. Note that its time to chaos is
, the SWB inside 24-bit RANLUX. Note that its time to chaos is 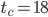 in the table below whereas Lüscher computed
in the table below whereas Lüscher computed 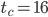 . If Lüscher miscalculated the time to chaos, then the average distance of two random vectors in the dynamical systems model would shrink from approximately 0.5 to at most
. If Lüscher miscalculated the time to chaos, then the average distance of two random vectors in the dynamical systems model would shrink from approximately 0.5 to at most 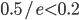 .
.
| Generator | Word size w | Long lag r | Short lag s | Time to chaos t_c | Base 2 logarithm of period length |
|---|---|---|---|---|---|
| AWC | 16 | 9 | 2 | 10 | 139 |
| 16 | 18 | 13 | 16 | 287 | |
| 32 | 8 | 3 | 22 | 255 | |
| 32 | 16 | 3 | 17 | 509 | |
| 32 | 29 | 17 | 27 | 927 | |
| 64 | 25 | 14 | 51 | < 1600 | |
| 64 | 28 | 11 | 44 | < 1792 | |
| SWB (Method II) | 32 | 19 | 16 | 32 | > 47 |
| 64 | 15 | 2 | 30 | 959 | |
| 64 | 17 | 14 | 62 | < 1088 | |
| 64 | 62 | 5 | 21 | > 165 | |
| SWB (Method I) | 16 | 5 | 3 | 15 | 71 |
| 16 | 11 | 3 | 11 | 169 | |
| 16 | 11 | 5 | 13 | 167 | |
| 24 | 10 | 24 | 18 | 570 | |
| 32 | 7 | 3 | 25 | 217 | |
| 32 | 16 | 9 | 27 | 506 | |
| 32 | 17 | 3 | 17 | 534 | |
| 32 | 21 | 6 | 19 | 664 | |
| 64 | 13 | 7 | 51 | 818 | |
| Generator | Word size w | Long lag r | Short lag s | Time to chaos t_c | Base 2 logarithm of period length |
RANLUX Implementation
Lower and Upper Bounds for the Period Length
There are arguments based on statistical considerations that an application should never deplete more than 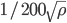 elements of the random sequence, see Thoughts on pseudorandom number generators by B. D. Ripley. Strong bounds on the period length arise if one wants to pass the empirical RNG birthday spacings test at all cost. One can show that his test becomes really powerful once more than
elements of the random sequence, see Thoughts on pseudorandom number generators by B. D. Ripley. Strong bounds on the period length arise if one wants to pass the empirical RNG birthday spacings test at all cost. One can show that his test becomes really powerful once more than ![\sqrt[3]{\rho}](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_4a8a77b628f4ef531e4005f92fde137d.gif) samples are used, cf. On the Interaction of Birthday Spacings Tests with Certain Families of Random Number Generators. Hence, bad generators can potentially avoid detection if they have a very long period.
samples are used, cf. On the Interaction of Birthday Spacings Tests with Certain Families of Random Number Generators. Hence, bad generators can potentially avoid detection if they have a very long period.
Based on the laws of thermodynamics and Landauer's principle, Aaron Toponce calculated the minimum amount of energy needed brute force encryption keys of a symmetric cipher in his article The Physics of Brute Force. He concluded that a superluminous supernova (a hypernova) provides enough energy to enter all states of a 227-bit integer once under ideal conditions. If we combine this fact with the thoughts regarding the birthday test, then all period lengths above 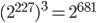 can be considered safe.
can be considered safe.
With respect to minimal period lengths B. D. Ripley recommended in his paper from 1989 cited above, a period length of at least 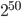 . If I imagine the scenario of drawing all 32-bit integer once from the PRNG in conjunction with the requirement to pass the birthday test, then
. If I imagine the scenario of drawing all 32-bit integer once from the PRNG in conjunction with the requirement to pass the birthday test, then 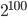 is a good lower bound on the period length. All RANLUX flavors of interest in the remainder of the text have a period of at least
is a good lower bound on the period length. All RANLUX flavors of interest in the remainder of the text have a period of at least 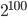 .
.
Implementing the Carry Flag
Reconsider the recurrence of an AWC: 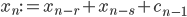 . In theory, one could generate a single random value at a time with an add-with-carry instruction. In practice, the execution will return to the caller site at some point meaning one would have to store carry flag or even the entire processor status register. Moreover, there is no such a thing as a carry flag in C and C++. Consequently, an AWC implementation must check for overflow or explicitly compute the carry bit.
. In theory, one could generate a single random value at a time with an add-with-carry instruction. In practice, the execution will return to the caller site at some point meaning one would have to store carry flag or even the entire processor status register. Moreover, there is no such a thing as a carry flag in C and C++. Consequently, an AWC implementation must check for overflow or explicitly compute the carry bit.
One approach is to use two additions and to check for overflow twice (if 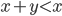 , then there was an overflow). This approach is easy to implement but I did not like it because branching usually incurs a significant overhead in modern processors. Instead I exploited the fact all the terms in the recurrence are native integer types with
, then there was an overflow). This approach is easy to implement but I did not like it because branching usually incurs a significant overhead in modern processors. Instead I exploited the fact all the terms in the recurrence are native integer types with 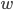 bits so just promoted
bits so just promoted 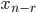 ,
, 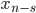 , to the next larger integer type in C++ and added them. The result is then a value with
, to the next larger integer type in C++ and added them. The result is then a value with 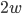 bits with
bits with 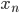 being in the lower
being in the lower 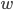 bits while the carry is in the upper
bits while the carry is in the upper 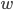 bits. We can recover
bits. We can recover 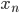 by truncating the result and the carry by shifting. In C++ with
by truncating the result and the carry by shifting. In C++ with 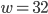 , this could be implemented as follows:
, this could be implemented as follows:
x := uint64_t(xs[n-r]) + xs[n-s] + carry xs[n] := uint32_t(x) carry := x >> 32
On 32-bit ISAs, the compiler could use an add- followed by an add-with-carry instruction to implement this sequence; no shift would be necessary to recover the carry since the carry would already be stored in its own register. On 64-bit ISAs, the compiler could re-use the same instruction sequence or 64-bit arithmetic.
The table below shows the CPU time of an AWC testing explicitly for overflow relative to the CPU time of an AWC promoting to the next larger integer type for different bases  . The first column shows the AWC parameters, the second column shows the relative timing on x86-64 with GCC-8.2.0, and the third column contains the data from Clang-3.5.0 on ARMv7-A; values above one imply the type promotion solution is faster, values below one imply explicit overflow checks are faster. We cannot use integer promotion on ARMv7-A when
. The first column shows the AWC parameters, the second column shows the relative timing on x86-64 with GCC-8.2.0, and the third column contains the data from Clang-3.5.0 on ARMv7-A; values above one imply the type promotion solution is faster, values below one imply explicit overflow checks are faster. We cannot use integer promotion on ARMv7-A when 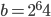 because there is no 128-bit integer type. Hence, this field stays empty.
because there is no 128-bit integer type. Hence, this field stays empty.
On x86-64 with GCC-8.2.0, checking the condition flag gives much faster code for 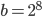 . In any other test, type promotion is faster. Beware that the performance difference narrows noticeably for larger long lags
. In any other test, type promotion is faster. Beware that the performance difference narrows noticeably for larger long lags 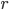 .
.
| Generator | ARMv7-A CPU time | x86-64 CPU time |
|---|---|---|
| AWC(2^8, 8, 5) | 1.24 | 0.69 |
| AWC(2^16, 9, 2) | 1.21 | 1.86 |
| AWC(2^32, 16, 3) | 1.06 | 1.10 |
| AWC(2^64, 25, 14) | -- | 1.03 |
The SWB recurrences can also be evaluated with the aid of larger integer types. If we promote the result of an evaluation to the next larger integer type, then the upper 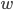 bits will contain the borrow which will be either zero or all ones if an underflow occurred, where all ones is the two's complement representation of -1. Thus, to extract the carry we must shift again, truncate, and negate the result
bits will contain the borrow which will be either zero or all ones if an underflow occurred, where all ones is the two's complement representation of -1. Thus, to extract the carry we must shift again, truncate, and negate the result
x := uint64_t(xs[n-r]) - xs[n-s] - carry xs[n] := uint32_t(x) carry := -uint32_t(x >> 32)
The approach using type promotion was implemented by me for all bases  including
including 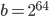 if an 128-bit integer type is available (this is the case in recent GCC and Clang releases). Otherwise the implementation resorts to explicit overflow checks.
if an 128-bit integer type is available (this is the case in recent GCC and Clang releases). Otherwise the implementation resorts to explicit overflow checks.
Next, I measured the speed of my Type II SWB implementation in comparison to the C+11 standard library implementation in the class subtract_with_carry_engine for different bases  . The first column shows the parameter tuples, the second and third column contain the time to compute one billion values with the C++11 standard library implementation relative to my code for ARMv7-A and x86-64, respectively. Values below one indicate that the GNU C++ Library (libstdc++) code consumes less CPU time. On ARMv7-A my code is consistently and distinctively slower than libstdc++ so I went to investigate how this could be possible. It turns out that if all bits of the integer type used inside
. The first column shows the parameter tuples, the second and third column contain the time to compute one billion values with the C++11 standard library implementation relative to my code for ARMv7-A and x86-64, respectively. Values below one indicate that the GNU C++ Library (libstdc++) code consumes less CPU time. On ARMv7-A my code is consistently and distinctively slower than libstdc++ so I went to investigate how this could be possible. It turns out that if all bits of the integer type used inside subtract_with_carry_engine are manipulated (e.g. 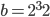 and
and uint32_t as integer type), then the carry bit may be set incorrectly when using libstdc++; this is GCC bug 89979. libc++ does not contain this bug.
| Generator | ARMv7-A CPU time | x86-64 CPU time |
|---|---|---|
| SWB(2^8, 3, 7) | 0.69 | 1.47 |
| SWB(2^16, 3, 11) | 0.90 | 1.10 |
| SWB(2^32, 3, 17) | 0.71 | 1.06 |
| SWB(2^64, 7, 13) | 0.90 | 0.88 |
As a rule of thumb, if two programs exhibit completely different performance characteristics, then there are either fundamental implementation differences or the programs solve different problems. Examples for the former are using compiled instead of interpreted code, employing hash tables instead of binary search trees, working with probabilistic instead of deterministic solvers, or running iterative instead of direct solvers. Examples for the latter are computing one solution instead of all of them, handling only special cases instead of the general case, or bugs.
On the one hand I cannot say how the performance of my implementation relates to libstdc++ because the algorithms in it cannot be used for the bases considered here. On the other hand, libc++ does work correctly but it is slower.
On a final note, given the short lag 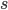 and base
and base 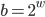 of an AWC, one can also exploit the carry bit to implement the recurrence using integers with
of an AWC, one can also exploit the carry bit to implement the recurrence using integers with 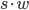 bits, e.g., with
bits, e.g., with 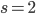 and
and 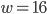 :
:
uint32_t x = 0 uint32_t y = 0 memcpy(&x, xs+n-s, 2*s) memcpy(&y, xs+n-r, 2*s) z := uint64_t(x) + y + carry memcpy(xs+n, &z, 2*s) carry := uint32_t(z >> 32)
The ranlux-tools repository contains  code using this trick in
code using this trick in prng-optimization.cpp.
Selecting a RANLUX Variant
In the preceding sections, I tried different AWC/SWB implementations and searched for good parameter combinations. Here, I will select AWC and SWB candidates for a fast RANLUX PRNG with 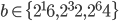 . So far, there was no benchmark comparing AWCs and SWBs. For this reason, I will pick one AWC and one SWB for every value of
. So far, there was no benchmark comparing AWCs and SWBs. For this reason, I will pick one AWC and one SWB for every value of  if the times to chaos are approximately equal.
if the times to chaos are approximately equal.
For my needs all period lengths are large enough. Therefore, I will pre-select generators with a time to chaos as small as possible:
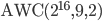 ,
, 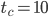 ,
,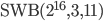 ,
, 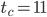 ,
,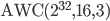 ,
, 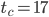 ,
,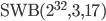 ,
, 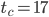 ,
,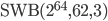 ,
, 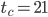 .
.
This pre-selection is already subjective because I do trade speed for size, e.g., 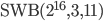 has
has 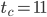 whereas
whereas 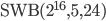 has
has 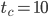 and a significantly larger long lag. I find this undesirable because the period is long enough for my needs in both cases (
and a significantly larger long lag. I find this undesirable because the period is long enough for my needs in both cases (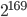 and
and 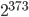 , respectively). Moreover, I searched only for SWBs with
, respectively). Moreover, I searched only for SWBs with 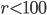 but larger long lags may reveal more interesting parameter combinations. The 64-bit PRNG is only possible choice with such a short time to chaos.
but larger long lags may reveal more interesting parameter combinations. The 64-bit PRNG is only possible choice with such a short time to chaos.
Based on Lüscher's discussion one needs to generously reject RNG values. Let  be a positive integer with
be a positive integer with 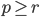 . For every
. For every  values drawn from the generator, one has to discard
values drawn from the generator, one has to discard 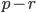 . I will call
. I will call  block size. We have to discard at least
block size. We have to discard at least 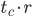 values after drawing
values after drawing 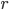 values but it is a good idea to round the number of discards up to the next larger prime number. This gives us the following RANLUX PRNG parameters (the squared brackets indicate the block size
values but it is a good idea to round the number of discards up to the next larger prime number. This gives us the following RANLUX PRNG parameters (the squared brackets indicate the block size  followed by the number of values to retain from each block):
followed by the number of values to retain from each block):
Experience has shown that 24-bit RANLUX passes all existing empirical tests with block sizes far below than what is required by the dynamical systems model. Specifically, 24-bit RANLUX with 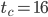 gives
gives 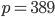 but a block size of 97 is already sufficiently large to have this generator pass common empirical RNG tests. Also, the time to chaos was determined to be
but a block size of 97 is already sufficiently large to have this generator pass common empirical RNG tests. Also, the time to chaos was determined to be 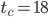 in the experiments here. Assuming that a block size of
in the experiments here. Assuming that a block size of 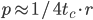 is large enough for practical applications, I also introduce the following RANLUX candidates:
is large enough for practical applications, I also introduce the following RANLUX candidates:
In the remainder of the text, I will say that generators with 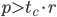 have full block size, otherwise they have reduced block size.
have full block size, otherwise they have reduced block size.
In the table below we compare for each base b the competing generators. The values in the table are the SWB CPU time divided by the AWC CPU time. The first column shows the base b, the second column shows if we discard no values (key "base"), as many values as necessary according to the time of chaos ("full"), or only a few ("fast"). The third column contains the relative CPU time for ARMv7-A and the fourth column the relative CPU time for x86_64.
| Generators | Block size | ARMv7-A CPU time | x86-64 CPU time |
|---|---|---|---|
| SWB(2^16, 3, 11) vs AWC(2^16, 9, 2) | (none) | 1.00 | 0.96 |
| reduced | 1.25 | 1.21 | |
| full | 1.10 | 1.14 | |
| SWB(2^32, 3, 17) vs AWC(2^32, 16, 3) | (none) | 1.03 | 0.96 |
| reduced | 1.05 | 0.97 | |
| full | 1.09 | 0.95 |
16-bit AWC outperforms its SWB counterpart on ARMv7-A as well as x86-64. Observe the pronounced difference for the reduced block size reflects quite well that one can use 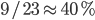 of all 16-bit AWC variates in comparison to
of all 16-bit AWC variates in comparison to 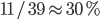 of the SWB values. 32-bit AWC is faster than 32-bit SWB on ARMv7-A but slower on x86-64.
of the SWB values. 32-bit AWC is faster than 32-bit SWB on ARMv7-A but slower on x86-64.
RANLUX Initialization
The following paragraphs contains the hints from Section 4.5 of the Marsaglia-Zaman paper, additional remarks from a paper called Common Defects in Initialization of Pseudorandom Number Generators, and C++11-specific comments.
Given base  and lags
and lags 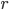 ,
, 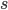 , the state of AWC/SWB generators consists of
, the state of AWC/SWB generators consists of 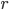 integers
integers 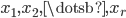 in the range
in the range 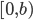 and a carry bit
and a carry bit  . There are two states which must be avoided because they cannot be escaped from:
. There are two states which must be avoided because they cannot be escaped from:
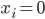 ,
, 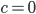 (all zeros), and
(all zeros), and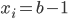 ,
, 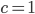 .
.
Not all of the remaining states are a part of a periodic sequence but this is not a problem because after at most 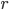 iterations, the generator state is guaranteed to be part of such a sequence. The recommendation is therefore to discard at least the first
iterations, the generator state is guaranteed to be part of such a sequence. The recommendation is therefore to discard at least the first 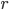 generator values right after selecting an initial state.
generator values right after selecting an initial state.
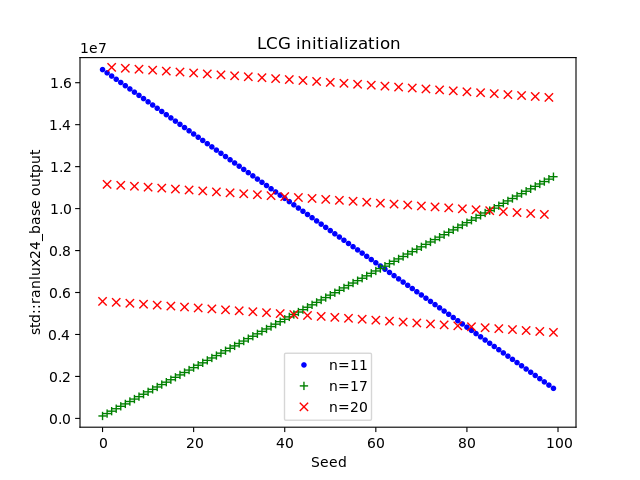
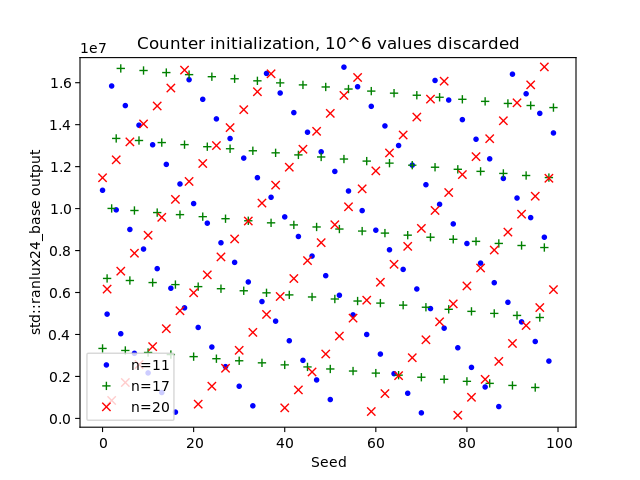
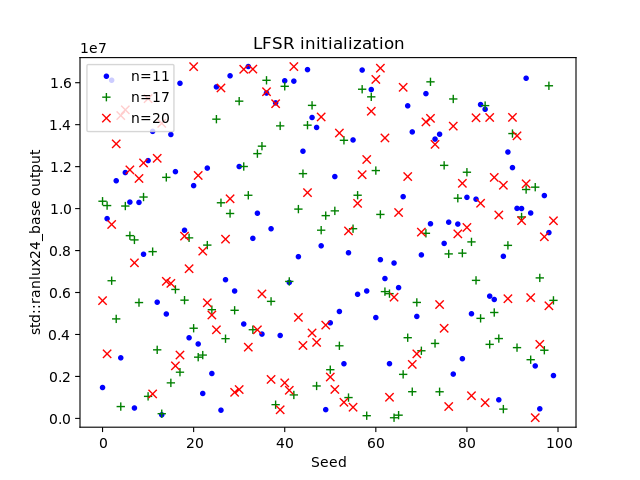
In general, the state can be initialized with any values including output from a second RNG as long as the the two unescapable states are avoided; let us call this second RNG the seed RNG. Usually it is desirable that different PRNG seeds lead to completely different output sequences and the paper Common Defects in Initialization of Pseudorandom Number Generators points out that, in layman's terms, this is not going to happen if the seed RNG is a pseudo-random number generator built on principles similar to the mathematical foundation of AWC/SWB generators. For example, the C++11 RANLUX RNGs are seeded by a linear congruential generator which possesses a mathematical structure similar to AWCs and SWBs. The effect can be seen in the figures below, where I plotted the eleventh, the 17th, and the 20th RANLUX generator value over the seeds one to 100. If different seeds cause completely different output sequences, then there will be very likely no discernible patterns in the figures. Yet in the plot below, there are very obvious patterns so different seeds do not yield completely different output sequences. Even worse, this behavior may persist indefinitely. In another experiment I initialized 24-bit RANLUX with 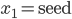 ,
, 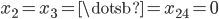 ,
, 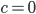 and discarded the first million values. There are still patterns visible in the output. If different seeds should cause completely different RANLUX sequences, then one has to initialize the state with a PRNG with a completely different mathematical structure, e.g., the Mersenne Twister, or with a true random number generator. The final plot below was created by utilizing a Mersenne Twister as seed RNG.
and discarded the first million values. There are still patterns visible in the output. If different seeds should cause completely different RANLUX sequences, then one has to initialize the state with a PRNG with a completely different mathematical structure, e.g., the Mersenne Twister, or with a true random number generator. The final plot below was created by utilizing a Mersenne Twister as seed RNG.
The plots do not show that that RANLUX is broken and they do not contradict Lüscher's analysis; they only exhibit the linear-affine behavior of AWCs and SWBs.
While I implemented add-with-carry generators, I decided to fix some shortcomings of the C++11 PRNG initialization. All C++11 standard library PRNG constructors take a 32-bit integer as seed and some PRNGs silently map this seed to a smaller range meaning different seeds may lead to the same initialization. My AWC/SWB implementations are supposed to use all possible values of 64-bit seed which made me look for a simple 32-bit PRNG with at least 64 bits of state and no unescapable states. After coming across xorshift PRNGs, I finally picked xoshiro128+ as seed generator. xoshiro128+ does have an unescapable state (all zeros) but the 128 bits of state allow me to use any 64-bit seed when initializing the remaining 64 bits with non-zero values.
C++11 Implementation
C++11 implements SWBs of the form SWB(b, s, r) in subtract_with_carry_engine. Values from this generator can be discarded automatically by the class discard_block_engine. Both classes can be found in the C++11 standard header random. The code below implements the pre-selected SWBs for 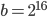 and
and 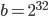 . The other generators can be found the ranlux-tools repository.
. The other generators can be found the ranlux-tools repository.
// Copyright 2019 Christoph Conrads // // This Source Code Form is subject to the terms of the // Mozilla Public License, v. 2.0. If a copy of the MPL was // not distributed with this file, You can obtain one at // http://mozilla.org/MPL/2.0/. #include <cstdint> #include <random> using ranlux16_base = std::subtract_with_carry_engine<std::uint16_t, 16, 3, 11>; using ranlux16 = std::discard_block_engine<ranlux16_base, 127u, 11u>; using fast_ranlux16 = std::discard_block_engine<ranlux16_base, 37u, 11u>; using ranlux32_base = std::subtract_with_carry_engine<std::uint32_t, 32, 3, 17>; using ranlux32 = std::discard_block_engine<ranlux32_base, 293u, 17u>; using fast_ranlux32 = std::discard_block_engine<ranlux32_base, 73u, 17u>;
Empirical Random Number Generator Testing
The quality of the variates of the new PRNGs was tested with TestU01 and DieHarder.
DieHarder was instructed to run all tests and to resolve ambiguous results with the command dieharder -a -g 200 -Y 1 -k2. ![\text{AWC}(2^{16}, 9, 2)[97, 9]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_4ee889c4ede774d011a33f9dc4f030eb.gif) ,
, ![\text{AWC}(2^{32}, 16, 3)[71, 16]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_143efc7e597941a0bbfb0e9949bdf684.gif) , and
, and ![\text{AWC}(2^{32}, 16, 3)[277, 16]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_8961da5bfa85b8a70192403f2199980f.gif) failed the "diehard_sums" test. The DieHarder documentation describes the reliability of it as "Do Not Use" and has the following to say about this test:
failed the "diehard_sums" test. The DieHarder documentation describes the reliability of it as "Do Not Use" and has the following to say about this test:
Similarly, the diehard sums test appears to produce a systematically non-flat distribution of p-values for all rngs tested, in particular for the "gold standard" cryptographic generators aes and threefish, as well as for the "good" generators in the GSL (mt19937, taus, gfsr4). It seems very unlikely that all of these generators would be flawed in the same way, so this test also should not be used to test your rng.
TestU01 is an empirical RNG test program using floating-point values. The floats were created with the aid of the C++11 standard library class uniform_float_distribution for the test battery BigCrush. ![\text{AWC}(2^{32}, 16, 3)[71, 16]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_143efc7e597941a0bbfb0e9949bdf684.gif) exhibited a suspiciously low p-value of
exhibited a suspiciously low p-value of 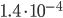 in the RandomWalk1 C test. All other tests were passed.
in the RandomWalk1 C test. All other tests were passed.
Benchmarks
Finally, we will compare new RANLUX variants to pseudo-random number generators in the C++11 standard library:
![\text{SWB}(2^{24}, 10, 24)[223, 23]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_d3af8146efd5e0f6b571b76d8c592c0e.gif) (class
(class std::ranlux24),![\text{SWB}(2^{48}, 5, 12)[389, 11]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_8557c20fdd4a1dbee5a5f7d276ef8166.gif) (
(std::ranlux48),- the Mersenne Twister with period length
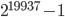 (
(std::mt19937), and - the 64-bit Mersenne Twister (
std::mt19937_64).
Additionally, xoshiro128+ was tested because it was already implemented for initializing the AWCs and SWBs. Observe that std::ranlux24 has a reduced block size though not as small as for the AWCs proposed above (the full block size at least 384 with 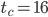 ).
).
The table below shows for each tested PRNG, the CPU time relative to the fastest PRNG (lower is better) as well as the throughput relative to the fastest generator (higher is better). Each row contains data of one random number engine. The first column shows the generator, the second and third column show CPU time and throughput, respectively, on an ARMv7-A processor, columns four and five contain the same data measured on x86-64.
| Generator | ARMv7-A CPU time | ARMv7-A Throughput | x86-64 CPU time | x86-64 Throughput |
|---|---|---|---|---|
| xoshiro128+ | 1.00 | 1.000 | 1.00 | 1.000 |
| std::mt19937 | 1.83 | 0.548 | 2.85 | 0.349 |
| std::mt19937_64 | 2.47 | 0.811 | 2.85 | 0.700 |
| AWC(2^32, 16, 3)[71,16] | 4.82 | 0.207 | 4.83 | 0.207 |
| SWB(2^64, 62, 3)[331,62] | 10.19 | 0.196 | 6.68 | 0.299 |
| AWC(2^32, 16, 3)[277,16] | 15.84 | 0.063 | 16.00 | 0.062 |
| SWB(2^64, 62, 3)[1303,62] | 36.79 | 0.054 | 24.12 | 0.083 |
| std::ranlux24 | 8.56 | 0.088 | 19.17 | 0.039 |
| std::ranlux48 | 43.20 | 0.035 | 71.56 | 0.021 |
xoshiro128+ is the fastest PRNG and possesses the highest throughput on both ARMv7-A and x86-64. The Mersenne Twisters are almost three times slower in the worst case although the 64-bit Mersenne Twisters achieves 71% to 81% of the xoshiro128+ throughput. The new RANLUX flavors with reduced block size rank right behind the Mersenne Twisters with respect to throughput which is 19%-30% of the maximum throughput. In terms of CPU time the ranking is similar with the exception of std::ranlux24 on ARMv7-A: it is faster than the 64-bit SWB with reduced block size. On x86-64, the new RANLUX generators with full block size have 6% to 8% of the xoshiro128+ throughput, they are up to 24 times slower, and std::ranlux24 is faster than the 64-bit SWB. On ARMv7-A, the new full-block size PRNGs deliver only 5% to 6% of the maximum throughput and they are up to 37 times slower. Moreover, std::ranlux24 performs better than both on ARMv7-A. Finally, std::ranlux48 is outclassed by every other PRNG. Restricting the discussion to generators with full block size, the next faster RNG after std::ranlux48 is at least 15% faster and has 50% higher throughput on ARMv7-A. On x86-64, std::ranlux48 is almost three times slower than 64-bit SWB and has less than third of the throughput of other full-period PRNGs.
In summary, among RANLUX PRNGs with full block size, the new generators are markedly faster while the new variants with reduced block size narrow the gap to other classes of PRNGs.
Conclusion
This blog post presents new parameter combinations for the RANLUX class of pseudo random-number generators. It introduces theory behind RANLUX generators including add-with-carry and subtract-with-borrow PRNGs, the dynamical systems point of view, and period length computation. Nowadays only one RANLUX variant based on a subtract-with-carry generators is in use. For this blog a comprehensive list of possible RANLUX parameters was assembled, different implementations are evaluated before presenting new RANLUX flavors that exhibit significantly better performance on current instruction set architectures while retaining all desirable properties of a RANLUX generator. The RANLUX PRNGs were implemented in C++11; they pass all DieHarder tests and the TestU01 BigCrush test battery.
Appendix
Open Source Contributions
This blog post spawned several contributions to open source projects.
Dieharder
A patch was submitted by me on April 9, 2019 fixing a compilation error because of a include in libdieharder.h (stdint.h is missing).
GNU Compiler Collection
Bug 89979 subtract_with_carry_engine incorrect carry flag
PractRand
PractRand crashes with GCC 8.2.0, most likely because GCC 8 assumes that all code paths in non-void functions contain a return statement. The patches in PractRand Bug #12 fix
- printf format flags,
- undefined behavior due to arithmetic shifts, and
- undefined behavior due to to a missing return statement.
Generator Variates
This section shows variates drawn from different AWCs and SWBs for testing purposes.
Add-with-Carry
Generator: 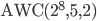
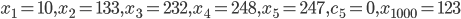
Subtract-with-Borrow (Method II)
Generator: 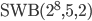
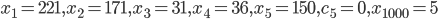
Subtract-With-Borrow (Method I)
Generator: 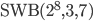
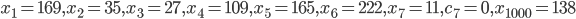
![\text{AWC}(2^{16}, 9, 2)[97,7]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_dec8f954110cfff89592a989b2ce44da.gif)
![\text{SWB}(2^{16}, 3, 11)[127,11]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_e846676db3a6975d640cc1718434e4ba.gif)
![\text{AWC}(2^{32}, 16, 3)[277,16]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_e1db4d0de2c58398d02c7f19920fc8ae.gif)
![\text{SWB}(2^{32}, 3, 17)[293,17]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_7bcbd50ec74d264ac0ddac7ac239d69c.gif)
![\text{SWB}(2^{64}, 62, 3)[1303,62]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_ddfbddbb48d98f782701531f0575f744.gif)
![\text{AWC}(2^{16}, 9, 2)[23,7]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_9fae092b49fc6c0436286aaee2b097ad.gif)
![\text{SWB}(2^{16}, 3, 11)[37,11]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_39a9e2e86dfcc1712806c6fd2d5eee99.gif)
![\text{AWC}(2^{32}, 16, 3)[71,16]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_0f9746c47823dee904f4a542918d7448.gif)
![\text{SWB}(2^{32}, 3, 17)[73,17]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_f40fd80f14362751622c7503d11f17dd.gif)
![\text{SWB}(2^{64}, 62, 3)[331,62]](https://christoph-conrads.name/wp-content/plugins/latex/cache/tex_fd340208076cd4ef3011e9038a0add53.gif)